Convergência

Foi feito um estudo sobre a convergência dos métodos númericos implementados. Dadas certas condições iniciais e um tempo de cálculo, calcula-se uma tabela para uma mesma trajetória utilizando diversos tamanhos de passo, partindo de valores grandes até passos mínimos. Cada linha da tabela têm a seguinte forma:

Linha $n$ = passo , r , $\frac{r_{n} - r_{n-1}}{r}$

$r$ pode ser calculado utilizando a distância em relação à posição inicial ou o comprimento total da trajetória.

Os valores de passo a serem utilizados nos cálculos da tabela são obtidos através do tempo de integração dividido por potências de 2, crescente a cada linha.

A última coluna desta tabela irá representar a convergencia do método de acordo com a variação de passo que esta sendo utilizada, no nosso caso potências de 2, o que irá induzir uma convergência quadrática.

Analisando os resultados da tabela para diversas condições iniciais, percebemos que os métodos de Runge Kutta e Runge Kutta Fehlberg aproximam para valores semelhantes, os métodos de Euler e Euler com Preditor e Corretor mostraram convergir mais lentamente e para um resultado um pouco diferente dos demais.

O método de Adams Moulton comportou-se de uma maneira semelhante ao Runge Kutta, mas seus valores finais não tem a mesma precisão, sendo este último aparentemente mais preciso. Mas o método de Adams tem a vantagem de ser mais rápido computacionalmente.

Segue o resultado de um dos testes: queda livre com velocidade inicial fixa:

Condições iniciais:

$$\begin{eqnarray*} X &=& 0\\ Y &=& 0\\ H &=& 500\\ \theta &=& 0\\ \sigma &=& 0\\ \psi &=& 0\\ V &=& 10\\ F_{N} &=& 0\\ F_{T} &=& 0\\ \\ \end{eqnarray*}$$

Tempo de cálculo = 100 segundos
$r$ = comprimento da trajetória

Euler 1a ordem:

-- passo --- r = comprimento --- $\frac{r_{n} - r{n-1}}{r_{n}}$ -
3.12500000 | 35182.12109375 | 0.000000e+00
1.56250000 | 46257.22656250 | 2.394221e-01
0.78125000 | 47860.58984375 | 3.349311e-02
0.39062500 | 48519.67968750 | 1.358212e-02
0.19531250 | 48803.69531250 | 5.819231e-03
0.09765625 | 48935.98437500 | 2.697401e-03
0.04882812 | 49000.03515625 | 1.306121e-03
0.02441406 | 49030.91406250 | 6.118588e-04
0.01220703 | 49046.72265625 | 3.058308e-04
0.00610352 | 49059.20312500 | 2.446024e-04

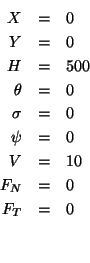
Euler com Preditor e Corretor 2a ordem:

-- passo --- r = comprimento --- $\frac{r_{n} - r{n-1}}{r_{n}}$ -
3.12500000 | 44132.34375000 | 0.000000e+00
1.56250000 | 47830.01953125 | 7.729455e-02
0.78125000 | 48372.91796875 | 1.120462e-02
0.39062500 | 48697.35546875 | 6.653339e-03
0.19531250 | 48875.38671875 | 3.641915e-03
0.09765625 | 48967.95703125 | 1.878780e-03
0.04882812 | 49015.09375000 | 9.588883e-04
0.02441406 | 49038.31640625 | 4.690210e-04
0.01220703 | 49050.40625000 | 2.446463e-04
0.00610352 | 49060.85156250 | 2.038285e-04

Adams Moulton 4a ordem

-- passo --- r = comprimento --- $\frac{r_{n} - r{n-1}}{r_{n}}$ -
3.12500000 | 41472.57421875 | 0.000000e+00
1.56250000 | 46546.69531250 | 1.090088e-01
0.78125000 | 48322.38281250 | 3.673246e-02
0.39062500 | 48788.22265625 | 9.530989e-03
0.19531250 | 48933.55078125 | 2.963202e-03
0.09765625 | 48998.63281250 | 1.326568e-03
0.04882812 | 49030.74218750 | 6.526518e-04
0.02441406 | 49046.32421875 | 3.058333e-04
0.01220703 | 49054.41796875 | 1.630842e-04
0.00610352 | 49062.78515625 | 1.630564e-04

Runge Kutta 4a ordem

-- passo --- r = comprimento --- $\frac{r_{n} - r{n-1}}{r_{n}}$ -
3.12500000 | 45293.58593750 | 0.000000e+00
1.56250000 | 47533.58984375 | 4.712457e-02
0.78125000 | 48299.84375000 | 1.585926e-02
0.39062500 | 48680.31250000 | 7.806031e-03
0.19531250 | 48871.33593750 | 3.908222e-03
0.09765625 | 48966.97656250 | 1.940083e-03
0.04882812 | 49014.83593750 | 9.588933e-04
0.02441406 | 49038.25000000 | 4.690216e-04
0.01220703 | 49050.39453125 | 2.446464e-04
0.00610352 | 49060.84765625 | 2.038285e-04

Runge Kutta fehlberg 5a ordem

-- passo --- r = comprimento --- $\frac{r_{n} - r{n-1}}{r_{n}}$ -
3.12500000 | 44504.02734375 | 0.000000e+00
1.56250000 | 47636.68359375 | 6.574765e-02
0.78125000 | 48300.20312500 | 1.372665e-02
0.39062500 | 48680.30859375 | 7.806031e-03
0.19531250 | 48871.33593750 | 3.908222e-03
0.09765625 | 48966.97656250 | 1.940083e-03
0.04882812 | 49014.83593750 | 9.588933e-04
0.02441406 | 49038.25390625 | 4.690216e-04
0.01220703 | 49050.39062500 | 2.446464e-04
0.00610352 | 49060.84765625 | 2.038285e-04

Percebeu-se que para valores de passo muito pequenos, menores que 1E-2, os métodos não convergiam de forma correta, constatou-se que isto se deve a precisão númerica dos dados no computador, fato que pode ser solucionado utilizando variáveis númericas de maior precisão, mas tendo como prejuízo uma maior demanda computacional e consequentemente um menor desempenho.