MAC-499: Trabalho de Formatura Supervisionado


Monografia


Implementações do Método de Aproximação Primal-Dual
aplicado ao Problema da Floresta de Steiner

Aluno: Rafael Pereira Luna
Supervisora: Cristina Gomes Fernandes



Resumo

Aqui, irei relatar os assuntos que estudei e um pouco da experiência que adquiri durante a minha iniciação científica, a qual teve início no mês de abril de 2002, sob a orientação da professora Cristina Gomes Fernandes. Esta monografia se divide em duas partes. Na primeira delas, é feita uma descrição do projeto que desenvolvi durante o ano. Na segunda parte, procurei relacionar a experiência obtida com a formação oferecida pelo BCC.


Índice



I - Descrição do Projeto


1 - Introdução

índice

Problemas de otimização combinatória têm aplicações nas mais diversas áreas, incluindo por exemplo projeto de redes de telecomunicação, de circuitos VLSI, empacotamento de objetos em containers, escalonamento e roteamento de veículos, etc. Vários destes problemas são reconhecidamente difíceis -- NP-difíceis -- e algoritmos de aproximação [1] são uma forma de atacá-los que têm recebido bastante atenção dentro de otimização combinatória na última década.

Dentre as várias técnicas de projeto de algoritmos de aproximação, uma se destaca por sua elegância e versatilidade: o método de aproximação primal-dual . Sofisticado, tal método deriva-se do método primal-dual clássico, que originou algoritmos exatos para problemas de fluxo em redes, de emparelhamento e de caminhos mais curtos.

O algoritmo de Bar-Yehuda e Even , de 1981, para o problema da cobertura por vértices, foi o primeiro uso (ainda que implícito) do método de aproximação primal-dual. Foram os trabalhos de Agrawal, Klein e Ravi  e de Goemans e Williamson , da década de 90, que retomaram e formalizaram o uso do método para o projeto de algoritmos de aproximação. Desde a publicação desses trabalhos, vários outros apareceram, tratando de problemas diferentes  ou de implementações alternativas que tornam o método mais eficiente .

O projeto de iniciação científica que desenvolvi durante o ano envolveu o estudo de tal método aplicado a um problema específico: o problema da floresta de Steiner. A próxima seção define este problema e a seguinte faz uso dele para explicar o método.


2 - O problema da floresta de Steiner

índice

Aqui, denotaremos o conjunto dos vértices e o conjunto das arestas de um grafo  G  por  VG  e  EG  , respectivamente. O problema da floresta de Steiner consiste no seguinte:

Problema: dados um grafo G, uma função custo c de  EG   nos racionais não-negativos e uma coleção R de subconjuntos de  VG  , encontrar uma R-floresta F que minimize $ c(F) = \sum_{e \in E_{F}} c_{e}$.

Os conjuntos da coleção R são chamados de conjuntos de terminais. Uma R-floresta F é uma floresta geradora de G que tem a seguinte propriedade: cada conjunto de terminais em R se encontra inteiramente contido no conjunto dos vértices de alguma das componentes de F  (uma floresta F de G é um subgrafo de G  que não contém ciclos; quando VF = VG , F é uma floresta geradora de G). Quando R está implícito, dizemos que uma floresta satisfazendo tal propriedade é uma floresta de Steiner de G. Note que podemos assumir que os conjuntos de R são dois a dois disjuntos (caso contrário, bastaria substituir cada par de conjuntos que não satisfaz esta restrição pela união dos conjuntos no par).

Eis um exemplo:




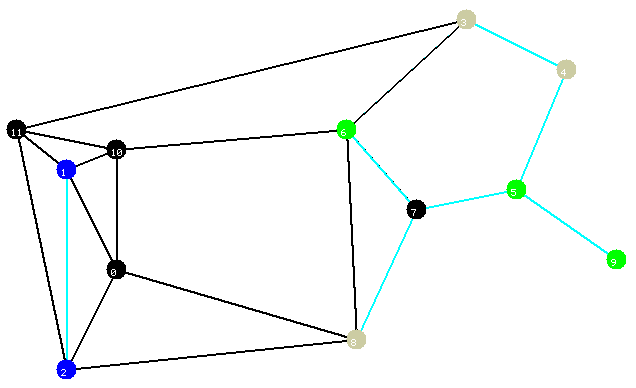
Figura 1


No grafo acima, a coleção R é formada por três conjuntos: o conjunto dos vértices azuis, o conjunto dos vértices cinzas e o conjunto dos vértices verdes. Os vértices pretos do grafo não estão em R ; tais vértices são chamados de vértices de Steiner. O custo de cada aresta é dado pela distância euclidiana entre seus extremos e as arestas em azul claro são as arestas de uma floresta de Steiner de custo mínimo.

O problema da floresta de Steiner pode ser classificado como um problema de projeto de redes. Esse tipo de problema consiste em exigir um certo grau de conexão entre determinados pares de vértices de um grafo. Uma aplicação prática do problema seria a seguinte: dado um certo conjunto de grupos de computadores, nós poderíamos estar interessados em conectar em rede os computadores dentro de cada grupo, usando no total a menor quantidade (comprimento) possível de cabo, sendo permitido instalar seletores ("switches" -- pontos não-terminais de conexão de cabos) apenas em pontos específicos. Neste caso, cada grupo de computadores poderia ser modelado através de um conjunto de terminais, os pontos nos quais é permitida a instalação de seletores seriam os vértices de Steiner do grafo e, por fim, o custo associado a cada conexão seria dado pela quantidade de cabo necessária para efetuar tal conexão. O problema também ocorre freqüentemente no projeto de circuitos VLSI.

Não se conhece um algoritmo eficiente (polinomial no tamanho da entrada G, c e R) para resolver o problema acima. Se a coleção R consiste em apenas um conjunto, o problema se reduz ao conhecido problema de Steiner em grafos , o qual é NP-difícil.


3 - O método de aproximação primal-dual

índice

É usual buscar-se bons algoritmos de aproximação para problemas de otimização NP-difíceis. Um algoritmo de aproximação para o problema da floresta de Steiner é um algoritmo polinomial que produz uma R-floresta F para a qual o valor de c(F) não dista muito do mínimo possível. Mais exatamente, denotemos por opt(G, c, R) o valor de c(F) para uma solução F do problema da floresta de Steiner. Seja k um racional, k maior ou igual a 1. Uma k-aproximação para o problema da floresta de Steiner é um algoritmo que recebe G, c e R como entrada e, em tempo polinomial no tamanho de G, c e R, produz uma R-floresta F tal que

$ c(F) \le k opt(G, c, R).$

Goemans e Williamson [2] propuseram uma 2-aproximação para o problema. Tal algoritmo baseia-se no método de aproximação primal-dual.

Um conceito fundamental no qual se apóia o algoritmo é o de conjunto ativo. Dados um grafo G e uma coleção R de conjuntos de terminais, um subconjunto S de  VG  é dito ativo se, e somente se, existe um conjunto T em R tal que

$ T \cap S \ne \emptyset$ e $ T \setminus S \ne \emptyset$.

Quando S é o conjunto dos vértices de alguma componente de uma floresta F de G, dizemos que tal componente é uma componente ativa de F; caso contrário a componente é dita inativa.

Note que uma floresta geradora F é uma R-floresta de G se, e somente se, $ E_{F} \cap \delta(S) \ne \emptyset$ para todo conjunto S ativo, onde $ \delta(S)$ é o corte determinado por S no grafo G. Assim, podemos enunciar o problema da floresta de Steiner na forma de um programa inteiro, como segue abaixo.

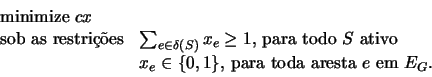
\begin{displaymath} \begin{array}{ll} \textrm{minimize $cx$} \\ \textrm{sob as... ...0, 1\} \textrm{, para toda aresta $e$\ em $E_{G}$.} \end{array}\end{displaymath}

Neste programa, x é um vetor indexado por  EG  e c é a função custo definida no problema. Note que toda floresta de Steiner do grafo G pode ser interpretada como uma solução viável do programa acima: dada uma floresta de Steiner F do grafo G, o vetor x tal que xe = 1  , para toda aresta e em  EF  , e  xe = 0  , para e em  EG \  EF , é uma solução viável do programa.

O programa linear abaixo é uma relaxação linear do programa inteiro.

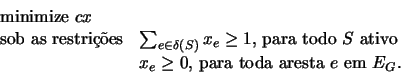
\begin{displaymath} \begin{array}{ll} \textrm{minimize $cx$} \\ \textrm{sob as... ...\geq 0 \textrm{, para toda aresta $e$\ em $E_{G}$.} \end{array}\end{displaymath}

O dual do programa acima é dado a seguir, onde y é um vetor indexado pela coleção de todos os conjuntos ativos de G.

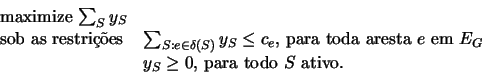
\begin{displaymath} \begin{array}{ll} \textrm{maximize $\sum_{S} y_{S}$} \\ \t... ...\\ & y_{S} \ge 0 \textrm{, para todo $S$\ ativo.} \end{array}\end{displaymath}

Em linhas gerais, o algoritmo parte de uma solução viável y do programa dual e, iterativamente, tenta ``melhorar'' esta solução até obter uma solução viável inteira x do programa primal que tenha custo igual a, no máximo, duas vezes o custo de uma solução ótima do problema da floresta de Steiner. Na verdade, no algoritmo, tal solução x é representada implicitamente por uma floresta geradora de G. Cada uma das iterações começa com uma floresta geradora de G; o algoritmo aumenta o valor das componentes de y correspondentes às componentes ativas desta floresta, fazendo com que a restrição do programa dual seja satisfeita com igualdade para algumas das arestas do grafo e, quando isto ocorre, uma dessas arestas é incluída na floresta. Quando todas as componentes da floresta corrente forem inativas o algoritmo termina, devolvendo uma subfloresta de Steiner minimal da floresta corrente.

Mais detalhadamente, cada iteração do algoritmo começa com uma floresta geradora de G que contém pelo menos uma componente ativa (e, portanto, o vetor x correspondente a esta floresta não satisfaz uma ou mais restrições do programa primal) e um vetor y, solução viável do programa dual. Na verdade, y não é armazenado explicitamente; ao invés disso, guarda-se o valor da função objetivo dual em y e, para cada vértice v do grafo, o número d(v) que é a soma das componentes de y correspondentes às componentes às quais v pertenceu nas florestas das iterações anteriores (incluindo a floresta corrente). A primeira iteração começa com uma floresta que não contém arestas, sendo composta por n componentes, onde n é o número de vértices do grafo (ou seja, cada vértice é uma componente da floresta). Além disso, y é igual ao vetor nulo.

Em cada iteração, uma aresta externa é incluída na floresta; uma aresta externa nada mais é do que uma aresta que une duas componentes distintas da floresta. A aresta externa escolhida pelo algoritmo para ser incluída na floresta é aquela que apresenta a menor folga (na verdade, pode haver mais de uma). O valor da folga de uma aresta uv é calculado da seguinte forma:

Em caso de empate, é dada preferência para arestas que tenham cada um dos extremos em uma componente ativa.

Uma vez que foi escolhida uma aresta, atualiza-se o custo da floresta (somando-se o custo da aresta incluída), o valor da função objetivo dual (somando-se a folga da aresta incluída multiplicada pelo número de componentes ativas) e o valor de d(v) para cada vértice v em uma componente ativa (somando-se a folga da aresta incluída).

O algoritmo pára quando todas as componentes da floresta estiverem inativas (o que ocorre após, no máximo, n - 1 iterações), devolvendo uma floresta de Steiner minimal contida na floresta corrente.

Abaixo, apresentamos, em pseudo-código, uma descrição não muito detalhada do algoritmo.

Algoritmo MinFS(G, R, c)
\begin{displaymath} \begin{array}{cl} 1 & F \leftarrow (V_{G} \textrm{, } \empty... ...inimal contida em } F\\ 10 & \textrm{devolva } F' \end{array}\end{displaymath}

O passo 9 do algoritmo é conhecido como passo de limpeza ou segunda fase do algoritmo.

Para uma melhor compreensão de seu funcionamento, vamos exibir agora uma simulação da execução do algoritmo sobre o grafo da Figura 1:





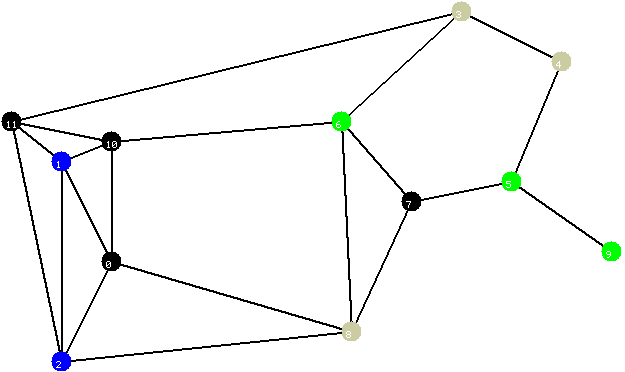
Figura 2



Em cada iteração do algoritmo, será desenhado, em torno de cada vértice v, um círculo com raio igual a d(v) (note que, inicialmente, cada círculo tem raio igual a zero; tal situação é ilustrada na Figura 2). Perceba que, deste modo, a folga de cada aresta externa uv pode ser interpretada como sendo o incremento, no raio, que é necessário para cobrir completamente uv com os círculos em torno de u e de v. Assim, se quando dois círculos se tocarem, existir no grafo uma aresta entre os dois vértices correspondentes, tal aresta será incluída na floresta corrente (pois ela será uma aresta de folga mínima), o que será indicado mudando a cor da aresta para azul claro. Na figura 3, exibimos o resultado da primeira iteração do algoritmo. Note que somente os círculos em torno de vértices em componentes ativas da floresta sofreram um incremento em seu raio (os círculos em torno dos vértices de Steiner continuam com raio zero) e que tal incremento é igual ao valor da folga mínima.





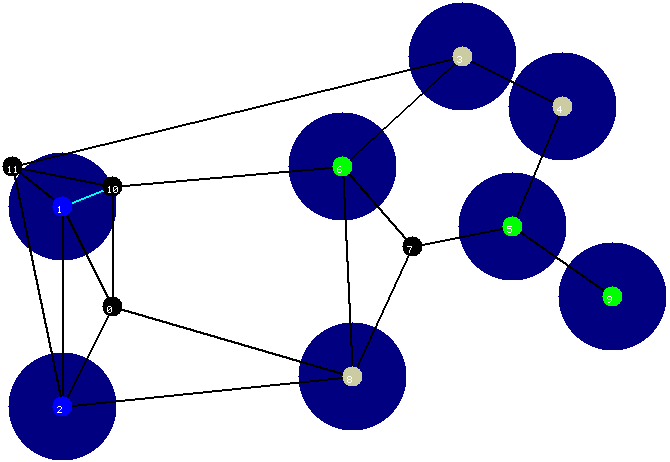
Figura 3



O resultado da segunda iteração é mostrado abaixo. Note que o raio dos círculos sofreu um incremento, o qual é representado pela fina camada cinza envolvendo cada círculo. Em conseqüência deste incremento, a aresta entre os vértices cinzas rotulados com os números 3 e 4 foi incluída na floresta.





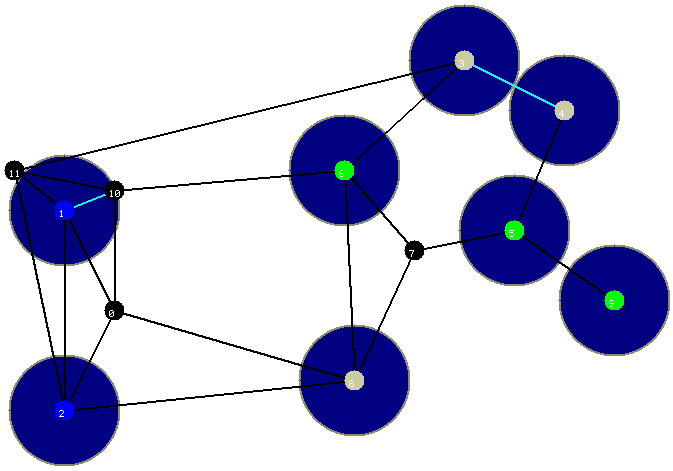
Figura 4



A figura abaixo ilustra a situação após a execução da terceira iteração. A aresta incluída é a aresta entre os vértices verdes 5 e 9. A camada verde em torno de cada círculo indica a folga da aresta no momento em que ela foi incluída na floresta.





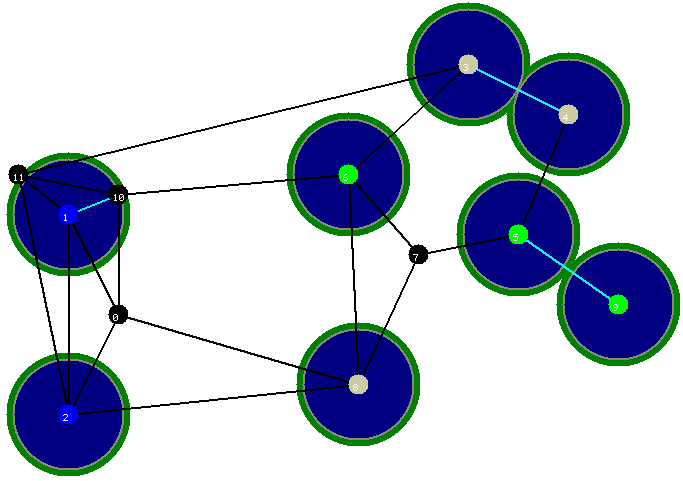
Figura 5



As próximas figuras ilustram a situação após a execução da quarta iteração...





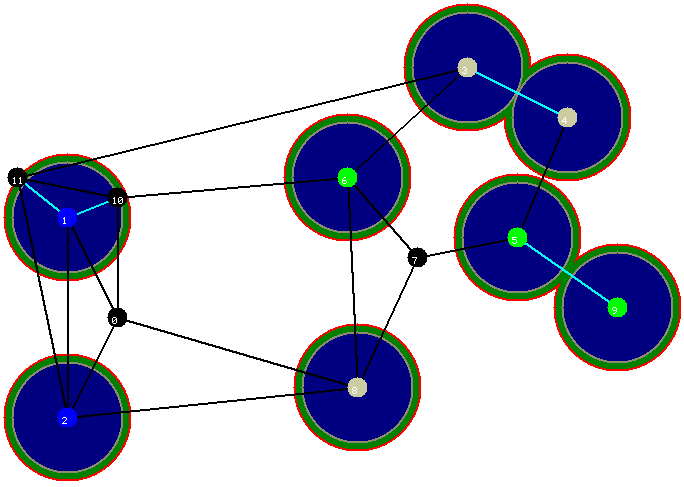
Figura 6



... quinta iteração...





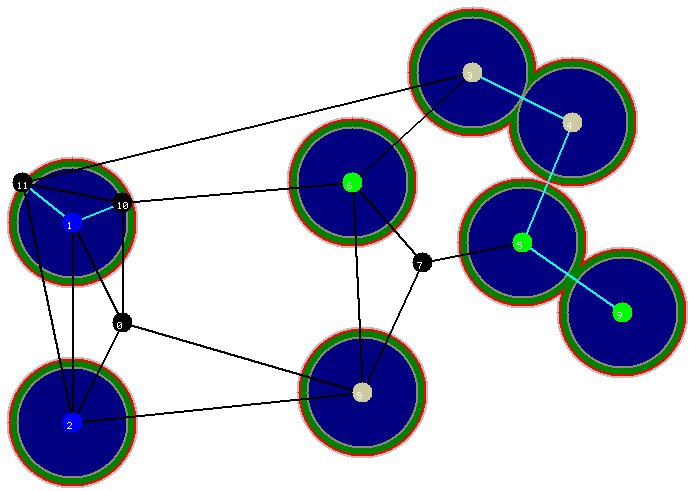
Figura 7



... e sexta iteração.





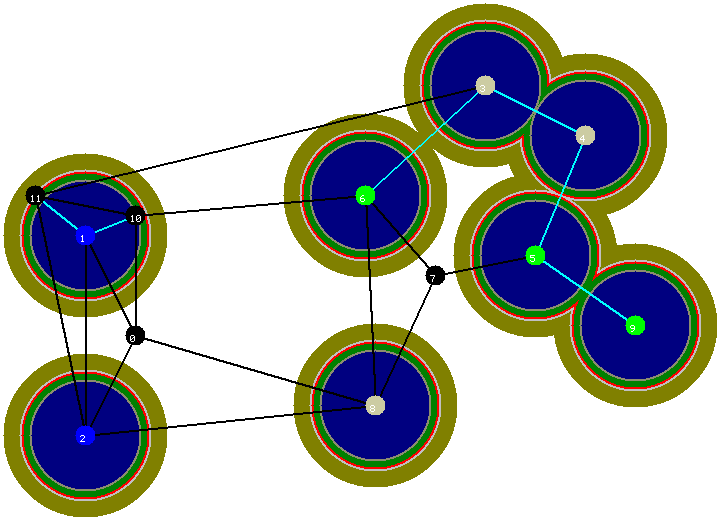
Figura 8



Na sétima iteração a aresta entre os vértices azuis 1 e 2 é incluída na floresta, o que faz com que a componente da floresta formada após esta inclusão seja uma componente inativa (pois esta componente "não separa" vértices terminais de uma mesma cor). Esta situação é ilustrada na figura abaixo.





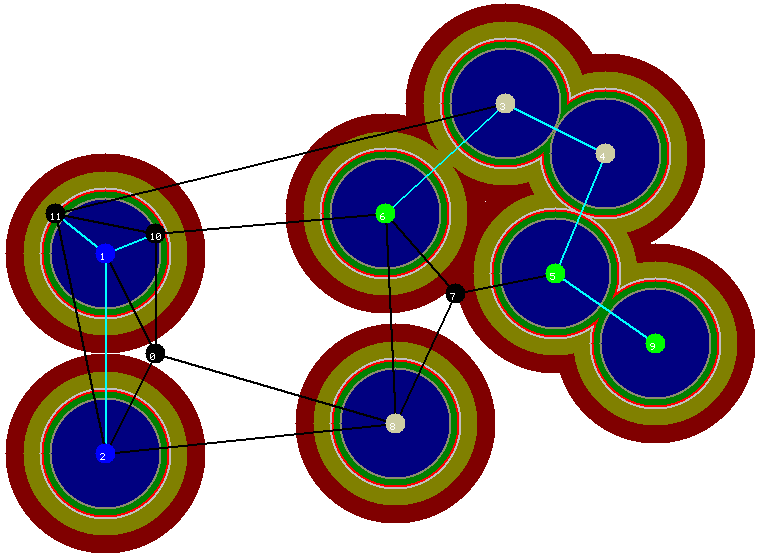
Figura 9



Como a componente contendo os vértices azuis é uma componente inativa, o raio dos círculos em torno dos vértices desta componente não será incrementado na oitava iteração do algoritmo (e nem nas próximas, neste nosso exemplo), a qual é ilustrada na figura abaixo. Os demais círculos terão seu raio incrementado (embora este incremento seja quase imperceptível na figura abaixo) e, desta forma, a aresta entre os vértices 5 e 7 será incluída na floresta.





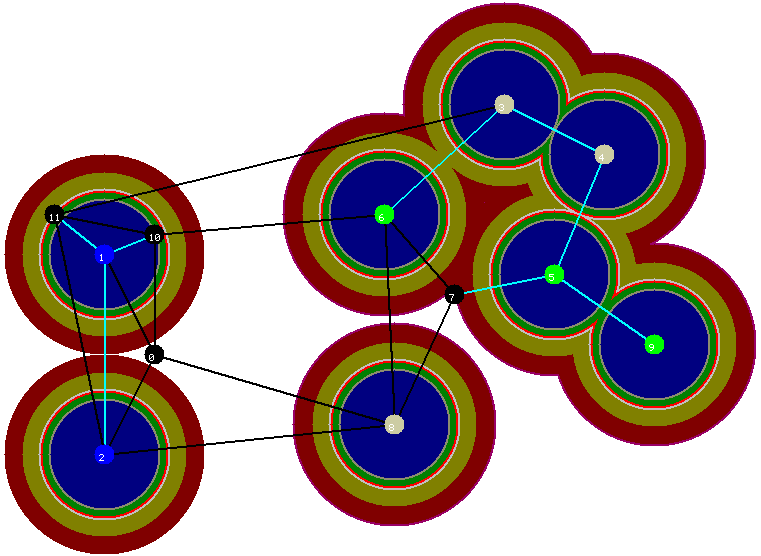
Figura 10



A nona e última iteração é ilustrada na figura abaixo. Note que todos os vértices terminais de uma mesma cor estão conectados através das arestas em azul claro e, deste modo, a floresta corrente é uma floresta de Steiner do grafo.





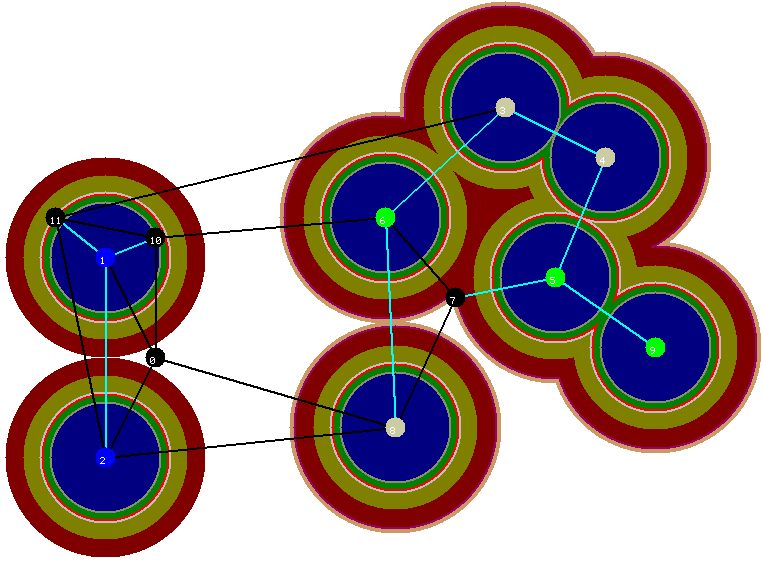
Figura 11



Na segunda fase do algoritmo, três arestas são eliminadas da floresta: as arestas entre os vértices 1 e 10, 1 e 11, e 5 e 7. A floresta resultante é uma floresta de Steiner minimal (pois a eliminação de qualquer aresta desta floresta desconecta dois vértices terminais de uma mesma cor), como mostra a figura abaixo.





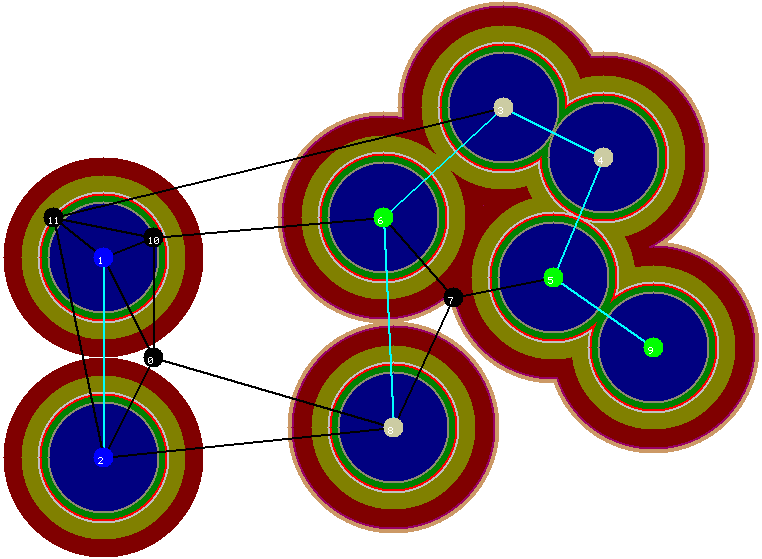
Figura 12



A floresta de Steiner devolvida pelo algoritmo é mostrada na figura abaixo. Note que esta floresta não é igual à floresta da Figura 1; na verdade, o custo dela é maior que o custo da floresta na Figura 1, a qual é ótima. Mais precisamente, o custo desta floresta é 1,023 vezes o custo de uma floresta de Steiner ótima (note que isto está de acordo com que o algoritmo promete, já que, no pior caso, ele devolve uma floresta de Steiner cujo custo é o dobro do custo de uma floresta de Steiner ótima).





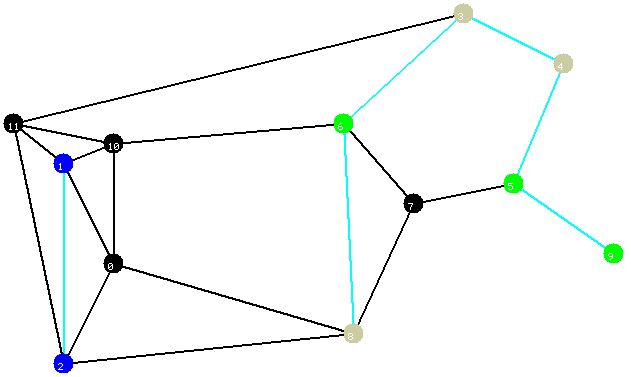
Figura 13




4 - Objetivos e metodologia empregada

índice

Fazer um estudo inicial de algoritmos de aproximação e, mais especificamente, do método de aproximação primal-dual para o problema da floresta de Steiner, através das diversas implementações propostas na literatura. Pretendia-se, além disso, fazer uma comparação experimental entre algumas destas implementações, por meio da construção de uma biblioteca, escrita na plataforma SGB (Stanford GraphBase [3]), com as diferentes implementações do método.


5 - Atividades realizadas e tópicos estudados

índice

As atividades tiveram início no final do mês de abril deste ano. Elas consistiram do estudo da teoria envolvida no projeto e de reuniões semanais com a orientadora, nas quais conversávamos sobre os assuntos estudados e definíamos os próximos passos a serem tomados dentro do projeto.

Inicialmente, as atividades envolveram o estudo de conceitos básicos sobre algoritmos de aproximação e de algumas das técnicas utilizadas para projetar estes algoritmos. Dentre estas técnicas estão aquelas que utilizam métodos clássicos de projeto de algoritmos como o método guloso e a programação dinâmica, e aquelas que envolvem conceitos e ferramentas de programação linear: os métodos de aproximação primal, dual e primal-dual.

A partir daí, me aprofundei nos estudos sobre o método de aproximação primal-dual e na aplicação deste método ao problema da floresta de Steiner. Tinha à minha disposição um projeto gráfico para demonstração do algoritmo de Goemans e Williamson para o problema da floresta de Steiner em instâncias euclidianas (onde cada vértice é um ponto do plano e o custo associado a cada aresta é dado pela distância euclidiana entre os seus extremos). Tal projeto, implementado em Java, foi feito por dois outros alunos como parte da disciplina MAC-5747 (Geometria Computacional). Juntamente com a minha orientadora, analisei o algoritmo implementado pelos alunos, constatando que este tinha complexidade O(n3) (n é o número de vértices no grafo de entrada) para grafos densos, ou seja, com muitas arestas (mais especificamente, a complexidade deste algoritmo é O(mn + n2), onde m é o número de arestas do grafo). Implementei, então, uma versão do algoritmo com complexidade O(n2log n), a qual foi incorporada ao projeto gráfico mencionado acima. Tal implementação utiliza várias filas de prioridade para tornar mais rápida a determinação de uma aresta de folga mínima.

Atualmente estou passando para a plataforma SGB a implementação O(n2log n) e convertendo-a para que funcione para grafos arbitrários. Além disso, estou fazendo um estudo inicial da implementação proposta Cole et al. [4].

Durante o desenvolvimento desse trabalho, percebemos uma maneira mais eficiente de implementar a segunda fase do algoritmo -- a fase de limpeza. Goemans e Williamson [2] sugerem que tal fase consome tempo O(n2) enquanto que Cole et al. [4] mencionam que não é difícil pensar em uma implementação que consuma tempo O(n log n). Ao que tudo indica, descobrimos uma maneira de implementar essa fase de forma que o consumo de tempo seja O(n). O algoritmo baseia-se em consultas pelo ancestral comum mais baixo de pares de vértices em uma árvore. Existem algoritmos lineares que pré-processam a árvore em questão, de forma a responder tais consultas em O(1)  [5, 6, 7]. Estudamos um destes algoritmos e, atualmente, estou concluíndo a sua implementação para, em seguida, integrá-la ao restante do projeto.


6 - Resultados e conclusão

índice

O projeto gráfico original desenvolvido pelos alunos da disciplina MAC-5747, juntamente com o texto que o analisa (escrito por mim) está disponível em:

http://www.ime.usp.br/~luna/steiner/joe-said/

A implementação em Java do algoritmo O(n2log n) para instâncias euclidianas do problema pode ser encontrada no site:

http://www.ime.usp.br/~luna/steiner/goemans-williamson/

A versão atual da implementação deste algoritmo para instâncias arbitrárias do problema, desenvolvida em CWEB e com o auxílio da plataforma SGB, pode ser encontrada em:

http://www.ime.usp.br/~luna/steiner/gw-cweb/

Inicialmente, eu havia planejado utilizar esta seção para, entre outras coisas, fazer comentários a respeito de uma comparação experimental entre duas implementações distintas do algoritmo de Goemans e Williamson: a implementação O(n2log n), citada na seção anterior, e a implementação proposta por Cole et al. [4]. Infelizmente, não foi possível realizar tal experimento devido ao fato de no último mês estar envolvido no estudo dos tópicos relacionados com o algoritmo que traz uma melhoria no desempenho da segunda fase do algoritmo, atividade esta que não estava prevista inicialmente. Em compensação, foi bastante gratificante descobrir que a segunda fase do algoritmo pode ser implementada em tempo O(n).


7 - Bibliografia

índice
  1. M.H. Carvalho, M.R. Cerioli, R. Dahab, P. Feofiloff, C.G. Fernandes, C.E. Ferreira, K.S. Guimarães, F.K. Miyazawa, J.C. Pina Jr., J. Soares, Y. Wakabayashi, Uma Introdução Sucinta a Algoritmos de Aproximação, Publicações Matemáticas do IMPA, 2001.

  2. M. Goemans e D. Williamson, A General Approximation Technique for Constrained Forest Problems, SIAM Journal on Computing, 24 (2), pp. 296-317, 1995.

  3. D. E. Knuth, The Stanford GraphBase: a platform for Combinatorial Computing, ACM Press, 1993.

  4. R. Cole, R. Hariharan, M. Lewenstein e E. Porat, A Faster Implementation of the Goemans-Williamson Clustering Algorithm, SODA 2001.

  5. D. Harel, R. Tarjan, Fast Algorithms for Finding Nearest Common Ancestors, SIAM Journal on Computing, 13, 2, 1984, pp. 338-355.

  6. B. Schieber, U. Vishkin, On Finding Lowest Common Ancestors: Simplification and Parallelization, SIAM Journal on Computing, 17, 6, 1988, pp. 1253-1262.

  7. Reif, John H., Synthesis of parallel algorithms, Morgan Kaufmann, 1993, cap. 6, pp. 259-271.


II - O BCC e a Experiência Adquirida com o Projeto


1 - Desafios e frustrações

índice

Desde o início do curso, planejei as disciplinas que cursaria em cada semestre de maneira que, no meu último ano de BCC, estivesse cursando poucas disciplinas para que, deste modo, pudesse ter tempo suficiente para me dedicar a um estágio ou iniciação científica. No final do ano passado, tomei a decisão de que faria o trabalho de formatura na forma de uma iniciação científica, pois tinha a intenção de fazer mestrado e queria utilizar a iniciação como uma prévia do que seria uma futura pós-graduação. Por incrível que pareça, o maior desafio que encontrei talvez tenha sido escolher a área em que faria a iniciação científica. No início do ano, estava em dúvida entre várias opções e, somente em abril, próximo da data limite de definição do supervisor nesta disciplina, é que eu consegui me decidir por uma delas.

Durante o desenvolvimento do projeto, não enfrentei nenhum grande problema ou desafio, pois, além de estar cursando poucas disciplinas durante o ano e, desta forma, ter tido tempo suficiente para me dedicar à iniciação científica, acredito que o curso me ofereceu toda a formação necessária para realizar as atividades envolvidas no projeto.

A minha maior frustração foi não ter conseguido atingir um dos objetivos do projeto, o qual era realizar um estudo comparativo, através de experimentos, entre pelo menos duas implementações para o algoritmo de Goemans e Williamson. Infelizmente, como já disse anteriormente, só foi possível fazer uma única implementação do algoritmo (a implementação O(n2log n) sugerida por Goemans e Williamson [2]) e iniciar o estudo teórico de uma outra (a implementação proposta por Cole et al. [4]).


2 - Interação com a orientadora

índice

Decidi fazer a iniciação científica em otimização combinatória, pois gostei bastante das disciplinas do curso relacionadas com a área. Escolhi a professora Cristina como minha orientadora na iniciação e supervisora em MAC-499, pois ela havia sido professora de MAC-338 (Análise de Algoritmos) no ano em que eu cursei a disciplina (2001) e, no momento, era professora da disciplina MAC-430 (Complexidade Computacional), a qual eu estava cursando.

Durante todo o desenvolvimento do projeto nos reuníamos uma vez por semana, na sala da professora. Nestas reuniões, eu contava à professora as atividades que eu havia realizado dentro do projeto e expunha eventuais dúvidas; além disso, conversávamos sobre a teoria envolvida no projeto e definíamos os próximos passos a serem tomados. A professora Cristina foi uma ótima orientadora, estando sempre disposta a atender minhas dúvidas, explicar a teoria envolvida e a revisar textos que eu produzi durante as atividades que desenvolvi dentro do projeto.


3 - Disciplinas mais relevantes

índice

Além das disciplinas como MAC-110 (Introdução à Computação), MAC-122 (Princípios de Desenvolvimento de Algoritmos), MAC-323 (Estruturas de dados), MAC-211 e MAC-242 (Laboratório de Programação I e II), nas quais adquiri as noções básicas de programação, as disciplinas que tiveram uma aplicação direta dentro das atividades envolvidas no projeto foram as seguintes:

A primeira (MAC-315) foi muito importante para o entendimento dos conceitos envolvidos com o método de aproximação primal-dual. Achei bastante interesssante estudar Programação Linear dentro do contexto do projeto, algo que só havia visto antes e, de uma maneira não muito aprofundada, durante a disciplina MAC-325.

Nas três disciplinas seguintes (MAC-328, MAC-338 e MAC325) aprendi os conceitos fundamentais sobre grafos, problemas de otimização em grafos, problemas de otimização em geral e análise de algoritmos. Tais conceitos foram imprecindíveis para o desenvolvimento do projeto.

A disciplina MAC-430 foi importante no sentido de que nela aprendi conceitos que me auxiliaram a compreender melhor qual a motivação de se projetar algoritmos de aproximação (a existência de problemas NP-difíceis, o que são exatamente esses problemas, etc). Por fim, em MAC-330, estudei alguns algoritmos (e implementei um deles como projeto da disciplina) que se baseavam em operações de manipulação de bits. Tal experiência foi bastante útil no momento de estudar e implementar o algoritmo para consulta do ancestral comum mais baixo entre dois vértices em uma árvore, o qual é utilizado para que segunda fase do algoritmo de Goemans e Williamson seja realizada em tempo linear.


4 - Considerações finais

índice

Gostei muito do projeto de iniciação científica que desenvolvi durante este ano. Por isto, pretendo continuar estudando o tema durante a pós-graduação que iniciarei no próximo ano, sob a orientação da professora Cristina. Inicialmente, o estudo será voltado ao problema da floresta de Steiner, visando uma compreensão mais rápida das diversas implementações do método de aproximação primal-dual descritas na literatura. Numa segunda fase, expandiremos o estudo, considerando alguns outros problemas para os quais o método de aproximação primal-dual também se aplica. Em princípio, os problemas que temos em mente são o problema de Steiner com coleta de prêmios (PCST - prize-collecting Steiner tree problem) e o problema de localização de centros distribuidores (FL - facility location problem).

Rafael Pereira Luna 2002-02-19