Monografia - Detalhes dos Tópicos Estudados
Aluno: Leo Kazuhiro Ueda
Supervisora: Nami Kobayashi
Projeto de Iniciação Científica
Autômatos Finitos: Algoritmos e Estruturas de Dados
Estudamos dois algoritmos para minimização de autômatos
finitos determinísticos, a versão de David Gries para
o algoritmo de John Hopcroft, com
complexidade de tempo
![]() , e o algoritmo
de Dominique Revuz para autômatos acíclicos, com
complexidade
, e o algoritmo
de Dominique Revuz para autômatos acíclicos, com
complexidade ![]() .
.
Começaremos com a definição do problema que queremos resolver, em seguida discutiremos os dois algoritmos.
Seja
![]() um autômato
finito determinístico.
um autômato
finito determinístico.
Queremos um algoritmo que determine um autômato
finito determinístico
![]() com o menor número de
estados e tal que
com o menor número de
estados e tal que
![]() .
Tal autômato é denominado minimal.
.
Tal autômato é denominado minimal.
Os métodos utilizados pelos dois algoritmos que
apresentamos aqui se baseiam na seguinte definição
de uma relação de equivalência sobre ![]() :
:
De modo muito simplificado, a idéia é encontrar
os estados equivalentes de
![]() .
Mais especificamente,
os algoritmos procuram pelas classes de
equivalência em Q, conforme a relação definida acima.
Sendo
.
Mais especificamente,
os algoritmos procuram pelas classes de
equivalência em Q, conforme a relação definida acima.
Sendo ![]() a classe de equivalência de
a classe de equivalência de ![]() ,
o autômato
,
o autômato
![]() definido da seguinte forma é minimal:
definido da seguinte forma é minimal:
Em [8], Hopcroft apresenta um algoritmo
para minimizar o número de estados de um autômato
finito determinístico, e afirma que ele tem
complexidade de tempo
![]() .
.
Até aquele momento, os algoritmos conhecidos levavam
tempo
![]() , ou mais, no pior caso.
Porém, a descrição do novo algoritmo e as suas provas
de corretude e complexidade de tempo foram consideradas
complicadas demais.
, ou mais, no pior caso.
Porém, a descrição do novo algoritmo e as suas provas
de corretude e complexidade de tempo foram consideradas
complicadas demais.
Por muitos anos, a despeito da importante melhora em relação
aos algoritmos clássicos, o algoritmo de Hopcroft foi praticamente
omitido de textos básicos sobre autômatos finitos.
Alguns apenas descreviam o algoritmo, mas sem mostrar as provas
de complexidade e corretude.
Muitos dos textos básicos [9,11] continuaram
a apresentar somente os algoritmos
![]() .
.
Com o objetivo de fornecer uma descrição mais clara, David Gries [7] re-descreve o algoritmo de Hopcroft, mas com uma pequena modificação. Apesar de ter cumprido seu objetivo, a descrição de Gries não se tornou muito popular.
Baseamos nosso estudo na descrição de Gries.
Analisaremos o algoritmo básico de forma a facilitar o entendimento do algoritmo final.
O algoritmo manterá uma partição de ![]() , que no início (ou final)
de cada iteração é aceitável.
Queremos que o algoritmo devolva uma partição onde
dois estados
, que no início (ou final)
de cada iteração é aceitável.
Queremos que o algoritmo devolva uma partição onde
dois estados ![]() e
e ![]() são equivalentes se e somente se
eles estão no mesmo bloco.
Os próximos dois lemas formalizam esse objetivo,
mostrando a situação inicial e final do algoritmo.
são equivalentes se e somente se
eles estão no mesmo bloco.
Os próximos dois lemas formalizam esse objetivo,
mostrando a situação inicial e final do algoritmo.
Portanto, podemos começar o algoritmo na situação do Lema 1 e fazer com que ele chegue à situação do Lema 2. O próximo lema descreve como fazer isso, refinando uma partição aceitável de uma maneira induzida pelas condições do Lema 2.
Seja
![]() uma partição aceitável.
Suponha que existem dois blocos
uma partição aceitável.
Suponha que existem dois blocos ![]() e
e ![]() , um símbolo
, um símbolo
![]() e dois estados
e dois estados ![]() e
e ![]() tais que:
tais que:
Então ![]() e
e ![]() não são estados equivalentes, e
podemos obter uma nova partição aceitável substituindo
não são estados equivalentes, e
podemos obter uma nova partição aceitável substituindo
![]() pelos blocos:
pelos blocos:
Essa substituição é na verdade uma divisão do bloco ![]() em dois blocos. Considerando novamente
em dois blocos. Considerando novamente
![]() , no bloco
, no bloco
![]() todos os arcos com rótulo
todos os arcos com rótulo ![]() que saem dele
chegam ao bloco
que saem dele
chegam ao bloco ![]() .
Da mesma forma, no bloco
.
Da mesma forma, no bloco
![]() ,
nenhum arco com rótulo
,
nenhum arco com rótulo ![]() chega ao bloco
chega ao bloco ![]() .
Note que esse é um refinamento do bloco
.
Note que esse é um refinamento do bloco ![]() em direção ao
nosso objetivo descrito no Lema 2.
Chamaremos essa operação de
divisão do bloco
em direção ao
nosso objetivo descrito no Lema 2.
Chamaremos essa operação de
divisão do bloco ![]() em relação ao par
em relação ao par ![]() ,
ou simplesmente
divisão de
,
ou simplesmente
divisão de ![]() em relação a
em relação a ![]() .
Veja a Figura 1.
.
Veja a Figura 1.
Usando os lemas vistos até agora, podemos escrever o
Algoritmo 4.
O algoritmo termina, pois a cada iteração um bloco é necessariamente
adicionado na partição, e não podemos ter mais do que ![]() blocos.
blocos.
Os lemas também podem mostrar que no final da execução do algoritmo, a partição obtida é a desejada.
Note que a ordem em que o Algoritmo (4)
faz as operações de divisão de blocos não importa para a corretude.
Então em cada iteração podemos determinar todas as
divisões em relação a ![]() e depois executar todas essas
divisões no mesmo passo.
Com isso teremos o Algoritmo 5.
e depois executar todas essas
divisões no mesmo passo.
Com isso teremos o Algoritmo 5.
Esse algoritmo não é muito eficiente, já que para verificar a
existência da tripla
![]() da condição do enquanto,
precisamos testar todas as triplas
da condição do enquanto,
precisamos testar todas as triplas
![]() existentes. Para esse teste somente, o algoritmo
precisa fazer pelo menos
existentes. Para esse teste somente, o algoritmo
precisa fazer pelo menos ![]() operações.
operações.
A estratégia para melhorar a complexidade é justamente
reduzir o tempo gasto na verificação da condição
do enquanto.
Faremos isso mantendo uma lista ![]() dos pares
dos pares
![]() em relação aos quais sabemos que
existem blocos
em relação aos quais sabemos que
existem blocos ![]() que precisam ser divididos.
Veremos a seguir como é possível manter
tal lista
que precisam ser divididos.
Veremos a seguir como é possível manter
tal lista ![]() .
.
Considere a seguinte observação:
Ou seja, qualquer bloco ![]() se encontrará na situação do bloco
se encontrará na situação do bloco
![]() ou do bloco
ou do bloco
![]() da Figura 1.
Isso nos leva ao seguinte lema:
da Figura 1.
Isso nos leva ao seguinte lema:
Com isso concluímos que um par ![]() só precisa
entrar na lista
só precisa
entrar na lista ![]() no máximo uma vez. Veja a Figura 2.
no máximo uma vez. Veja a Figura 2.
O próximo lema descreve um fato importante para a redução da complexidade.
A cada vez que o algoritmo divide os blocos em relação a um par
![]() , novos blocos são criados na partição.
Certamente haverá blocos que precisarão ser divididos em
relação aos novos blocos, portanto eles devem entrar
na lista
, novos blocos são criados na partição.
Certamente haverá blocos que precisarão ser divididos em
relação aos novos blocos, portanto eles devem entrar
na lista ![]() .
Apoiado no Lema 5,
o algoritmo tentará inserir os pares dos blocos menores.
.
Apoiado no Lema 5,
o algoritmo tentará inserir os pares dos blocos menores.
O seguinte lema é uma conseqüência do anterior e nos diz como
inicializar a lista ![]() .
.
Temos então o Algoritmo 7,
que usa a lista ![]() conforme
discutido.
conforme
discutido.
Comparando com o Algoritmo 5,
observa-se que a diferença está
na escolha do par ![]() .
Para essa escolha, o novo algoritmo manipula a lista
.
Para essa escolha, o novo algoritmo manipula a lista ![]() .
.
O Algoritmo 7 termina, pois
o número de pares ![]() é limitado;
cada par entra na lista
é limitado;
cada par entra na lista ![]() no máximo uma vez; e
a cada iteração removemos um elemento da lista
no máximo uma vez; e
a cada iteração removemos um elemento da lista ![]() .
Uma discussão sobre a corretude desse algoritmo pode ser
vista em ****relatório****.
.
Uma discussão sobre a corretude desse algoritmo pode ser
vista em ****relatório****.
Para analisar a complexidade do algoritmo, precisamos
detalhar mais os passos c e e.
Isso é feito no Algoritmo 8, visto
mais adiante.
Não discutiremos os detalhes das provas de complexidade de tempo, apenas faremos as seguintes observações:
Uma discussão um pouco mais completa pode ser vista em ****relatório****.
Em resumo, apresentamos as complexidades de tempo totais de cada passo do Algoritmo 8.
| Passo | Complexidade |
| b |
|
| c |
|
| d |
|
| e |
|
| f |
|
| Total |
|
Um autômato determinístico
![]() é acíclico se o grafo
é acíclico se o grafo
![]() é acíclico.
Autômatos determinísticos acíclicos são bastante usados para representar
dicionários [3] e manipular funções booleanas [4].
é acíclico.
Autômatos determinísticos acíclicos são bastante usados para representar
dicionários [3] e manipular funções booleanas [4].
O algoritmo de minimização que veremos a seguir tem grande
importância para essas aplicações, pois além de diminuir
o espaço em memória utilizado e agilizar as buscas
com autômatos, ele tem complexidade de tempo ![]() .
.
O nosso estudo foi baseado em [12].
Na definição do problema muda apenas a
entrada, que é restrita a autômatos finitos
determinísticos acíclicos.
Portanto, a entrada é um autômato acíclico
![]() .
Com isso, o autômato não deve ser completo,
isto é,
.
Com isso, o autômato não deve ser completo,
isto é, ![]() é uma função parcial.
é uma função parcial.
Como já foi mencionado, um autômato acíclico
![]() é um
autômato cujo grafo associado
é um
autômato cujo grafo associado
![]() é acíclico.
é acíclico.
Seja
![]() uma seqüência de palavras.
Vamos definir o prefixo comum de
uma seqüência de palavras.
Vamos definir o prefixo comum de ![]() como
sendo a seqüência
como
sendo a seqüência
![]() definida
da seguinte maneira. Seja
definida
da seguinte maneira. Seja
O comprimento do prefixo comum de ![]() é a soma dos comprimentos
das palavras em
é a soma dos comprimentos
das palavras em ![]() .
Essa definição será útil para a análise de complexidade de tempo
do algoritmo.
.
Essa definição será útil para a análise de complexidade de tempo
do algoritmo.
A altura de um estado ![]() do autômato acíclico
do autômato acíclico
![]() , ou
, ou ![]() , é o tamanho
do caminho de maior comprimento que começa em
, é o tamanho
do caminho de maior comprimento que começa em ![]() e chega a um estado final.
Mais formalmente,
e chega a um estado final.
Mais formalmente,
![]() .
.
Essa função altura induz uma partição
![]() de
de ![]() :
:
![]() será o conjunto ou bloco de estados de altura
será o conjunto ou bloco de estados de altura ![]() .
Diremos que conjunto
.
Diremos que conjunto ![]() é distinto se nenhum
par de estados em
é distinto se nenhum
par de estados em ![]() é equivalente.
é equivalente.
A idéia do algoritmo é simples.
Dado o autômato acíclico
![]() ,
a partição
,
a partição ![]() é calculada e cada estado
é calculada e cada estado ![]() é nomeado com uma
palavra que descreve as suas transições
é nomeado com uma
palavra que descreve as suas transições
![]() .
Os nomes dos estados são dados de tal forma que dois
estados possuem nomes iguais se e somente se
eles são equivalentes.
Portanto, o algoritmo
percorre os blocos
.
Os nomes dos estados são dados de tal forma que dois
estados possuem nomes iguais se e somente se
eles são equivalentes.
Portanto, o algoritmo
percorre os blocos
![]() nessa ordem,
aplicando uma ordenação
lexicográfica nos nomes dos estados de cada bloco
nessa ordem,
aplicando uma ordenação
lexicográfica nos nomes dos estados de cada bloco ![]() ,
e dessa forma encontrando os estados com nomes iguais.
Os estados equivalentes são então unidos, formando um
único estado.
A nomeação dos estados é feita uma única vez em cada estado,
e a ordenação é feita em tempo linear, logo, a
complexidade de tempo total é linear no número de transições
(
,
e dessa forma encontrando os estados com nomes iguais.
Os estados equivalentes são então unidos, formando um
único estado.
A nomeação dos estados é feita uma única vez em cada estado,
e a ordenação é feita em tempo linear, logo, a
complexidade de tempo total é linear no número de transições
(![]() ).
).
A dificuldade maior está em criar os nomes de forma que o gasto total com as ordenações seja de fato linear. Embora o algoritmo de ordenação em si seja linear no tamanho da entrada, o tamanho dos nomes poderia não ser linear em relação ao tamanho do autômato.
A seguinte propriedade relaciona a função altura com a equivalência dos estados.
A Figura 5 mostra um exemplo onde a
Propriedade 7 pode ser vista.
O bloco ![]() (
(![]() ),
que está abaixo de
),
que está abaixo de ![]() (
(![]() ), é distinto.
Pelas transições, podemos ver que
os estados
), é distinto.
Pelas transições, podemos ver que
os estados ![]() e
e ![]() são equivalentes (e o estado
são equivalentes (e o estado ![]() não é).
não é).
Com essa propriedade, é possível construir
um algoritmo simples.
Primeiro devemos criar a partição ![]() induzida pelas alturas.
Isso é feito percorrendo
induzida pelas alturas.
Isso é feito percorrendo
![]() como
em uma busca em profundidade.
A complexidade desse passo é
como
em uma busca em profundidade.
A complexidade desse passo é
![]() , onde
o número de transições
, onde
o número de transições ![]() é no máximo
é no máximo ![]() .
Em seguida, para cada nível encontramos
os estados equivalentes através da ordenação lexicográfica.
Veja o Algoritmo 9.
.
Em seguida, para cada nível encontramos
os estados equivalentes através da ordenação lexicográfica.
Veja o Algoritmo 9.
A Propriedade 7 pode mostrar que esse algoritmo é correto. Ademais, podemos executar o passo de união dos estados integrado ao passo da ordenação. Isso nos permite enunciar o seguinte lema:
Portanto, tentaremos usar um algoritmo de ordenação ![]() ,
como veremos a seguir.
,
como veremos a seguir.
Para a ordenação, nomearemos cada estado com uma palavra e aplicaremos uma ordenação lexicográfica. Essa ordenação consiste de várias aplicações de um outro algoritmo conhecido como bucket sort. Note que o algoritmo que usaremos é um pouco mais simples, pois queremos apenas distingüir os elementos.
Ordena uma seqüência
![]() de
inteiros
de
inteiros
![]() executando os
seguintes passos:
executando os
seguintes passos:
Ordena uma seqüência
![]() de
de ![]() -uplas
-uplas
![]()
![]() ,
onde
,
onde
![]() .
No primeiro passo, aplica-se o algoritmo bucket sort na
seqüência
.
No primeiro passo, aplica-se o algoritmo bucket sort na
seqüência ![]() considerando o
considerando o ![]() -ésimo inteiro de cada
-ésimo inteiro de cada
![]() -upla, ou seja, o bucket sort
considerará a seqüência
-upla, ou seja, o bucket sort
considerará a seqüência
![]() , mas
ordenará na verdade a seqüência
, mas
ordenará na verdade a seqüência ![]() .
O próximo passo considerará o
.
O próximo passo considerará o ![]() -ésimo inteiro de cada
-ésimo inteiro de cada ![]() e a seqüência
e a seqüência ![]() já ordenada de acordo com o
já ordenada de acordo com o ![]() -ésimo inteiro.
Portanto, por indução, a seqüência final é a seqüência
-ésimo inteiro.
Portanto, por indução, a seqüência final é a seqüência ![]() ordenada.
ordenada.
A complexidade de tempo é ![]() e o espaço em
memória é
e o espaço em
memória é ![]() .
.
A generalização da ordenação lexicográfica
para seqüências de ![]() -uplas de
tamanho variável, entre
-uplas de
tamanho variável, entre ![]() e
e ![]() , é feita
ordenando-se primeiro pelo tamanho das
, é feita
ordenando-se primeiro pelo tamanho das ![]() -uplas e
em seguida aplicando-se as ordenações, com
uma pequena diferença.
Quando o algoritmo considera o
-uplas e
em seguida aplicando-se as ordenações, com
uma pequena diferença.
Quando o algoritmo considera o ![]() -ésimo inteiro
apenas as
-ésimo inteiro
apenas as ![]() -uplas com pelo menos
-uplas com pelo menos ![]() inteiros
são ordenadas.
inteiros
são ordenadas.
Uma descrição completa desse algoritmo pode ser encontrada em [2]. Com um pouco mais de sofisticação, esse algoritmo pode ser melhorado aplicando-se os bucket sorts da esquerda para a direita. Não explicaremos os detalhes aqui, mas usaremos essa idéia no Algoritmo 10, mostrado mais adiante.
Eis o que o Algoritmo 10 faz.
Vamos tentar finalmente juntar
o Algortimo 10
ao Algoritmo 9 para
obtermos um algoritmo linear.
Para isso é preciso discutir a nomeação
dos estados.
Cada estado ![]() receberá um rótulo, definido
da seguinte maneira.
receberá um rótulo, definido
da seguinte maneira.
onde ![]() ou
ou ![]() diz se o estado
diz se o estado ![]() é final ou não,
é final ou não,
![]() é o símbolo do
é o símbolo do ![]() -ésimo arco, e
-ésimo arco, e ![]() é
um identificador (número) do estado apontado pelo
é
um identificador (número) do estado apontado pelo
![]() -ésimo arco.
A subseqüência
-ésimo arco.
A subseqüência
![]() deve estar ordenada.
deve estar ordenada.
De acordo com o Lema 8,
com esses rótulos nós obteremos
uma complexidade de
tempo
![]() no total,
onde
no total,
onde ![]() é o comprimento do prefixo comum
dos rótulos dos estados de altura
é o comprimento do prefixo comum
dos rótulos dos estados de altura ![]() .
Portanto, para obtermos a linearidade,
precisamos limitar o tamanho dos rótulos, que de certa forma
dependem da representação dos valores
.
Portanto, para obtermos a linearidade,
precisamos limitar o tamanho dos rótulos, que de certa forma
dependem da representação dos valores ![]() , os
números dos estados.
Por exemplo:
, os
números dos estados.
Por exemplo:
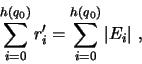
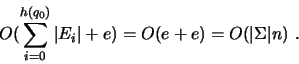
É possível diminuir o limitante para o
tamanho do vetor ![]() com uma
renumeração dos estados.
A idéia é reutilizar os números a cada
ordenação.
Para isso, um estado só receberá um número
se ele for usado.
com uma
renumeração dos estados.
A idéia é reutilizar os números a cada
ordenação.
Para isso, um estado só receberá um número
se ele for usado.
Os detalhes dessa técnica podem ser vistos em ****relatório****.
Com isso, o tamanho do vetor ![]() fica limitado por
fica limitado por
![]() .
.
Finalmente, o Algoritmo 11 mostrado
a seguir é a versão final.
A Figura 6 mostra um momento da execução do algoritmo,
quando ![]() e
e ![]() .
Podemos ver, pelos buckets, que os estados
.
Podemos ver, pelos buckets, que os estados ![]() e
e ![]() estão
prestes a ser unidos.
estão
prestes a ser unidos.
Neste projeto estudamos também um problema particular de busca
de padrões em textos.
Trata-se do caso em que o padrão é um conjunto finito ![]() de
palavras.
de
palavras.
O nosso estudo foi centrado no algoritmo clássico de Alfred Aho e Margaret Corasick. Em [1] eles apresentam o algoritmo, tendo como motivação a otimização de um sistema de consulta a um banco de dados de referências bibliográficas. Os resultados em relação aos algoritmos convencionais da época foram excelentes. Outras descrições do algoritmo podem ser encontradas em [5,6].
Vamos então descrever o problema e o modelo de solução,
que envolve a construção de um autômato finito determinístico
que representa as palavras em ![]() .
Para essa construção foram aplicadas
algumas idéias do algoritmo KMP,
de Knuth, Morris e Pratt [10].
Esse algoritmo resolve o problema da busca de
padrões para o caso em que o padrão é uma palavra.
.
Para essa construção foram aplicadas
algumas idéias do algoritmo KMP,
de Knuth, Morris e Pratt [10].
Esse algoritmo resolve o problema da busca de
padrões para o caso em que o padrão é uma palavra.
Seja
![]() um
conjunto finito de palavras em
um
conjunto finito de palavras em ![]() ,
as quais chamaremos de palavras-chave,
e
,
as quais chamaremos de palavras-chave,
e ![]() , também em
, também em ![]() , uma palavra qualquer
que chamaremos de texto.
O problema que queremos resolver é
localizar e identificar todos os fatores de
, uma palavra qualquer
que chamaremos de texto.
O problema que queremos resolver é
localizar e identificar todos os fatores de ![]() que são
também palavras-chave.
que são
também palavras-chave.
Para isso, utilizaremos um autômato
que reconhece a linguagem ![]() .
O autômato recebe como
entrada o texto
.
O autômato recebe como
entrada o texto ![]() e gera uma saída
contendo as posições em
e gera uma saída
contendo as posições em ![]() onde alguma palavra-chave
aparece como fator.
Essa fase é a busca propriamente dita,
e sua complexidade de tempo é
onde alguma palavra-chave
aparece como fator.
Essa fase é a busca propriamente dita,
e sua complexidade de tempo é ![]() , dependendo
da implementação da função de transição.
Note que esse tempo não depende do número de
palavras-chave.
, dependendo
da implementação da função de transição.
Note que esse tempo não depende do número de
palavras-chave.
Há também a fase de construção do autômato.
Ela é feita em duas etapas, em tempo ![]() no total,
onde
no total,
onde ![]() é a soma dos comprimentos das
palavras em
é a soma dos comprimentos das
palavras em ![]() e
e
![]() é o conjunto
dos símbolos que ocorrem em
é o conjunto
dos símbolos que ocorrem em ![]() .
A primeira etapa consiste em construir,
a partir do conjunto
.
A primeira etapa consiste em construir,
a partir do conjunto ![]() ,
uma máquina de estados muito semelhante
a um autômato finito determinístico.
Essa construção utiliza as idéias do
algoritmo KMP, e pode ser feita em tempo
,
uma máquina de estados muito semelhante
a um autômato finito determinístico.
Essa construção utiliza as idéias do
algoritmo KMP, e pode ser feita em tempo
![]() , dependendo da implementação.
Em seguida, a partir da máquina de estados,
obtém-se em
tempo
, dependendo da implementação.
Em seguida, a partir da máquina de estados,
obtém-se em
tempo ![]() o autômato finito determinístico,
que reconhece a linguagem
o autômato finito determinístico,
que reconhece a linguagem ![]() .
.
Portanto, o tempo de construir e aplicar a máquina de estados
é ![]() .
Note que aplicando o algoritmo KMP
.
Note que aplicando o algoritmo KMP ![]() vezes
com entrada
vezes
com entrada ![]() ,
uma vez para cada palavra em
,
uma vez para cada palavra em ![]() , a complexidade
total de pior caso seria
, a complexidade
total de pior caso seria ![]() .
.
Como já mencionamos, o algoritmo funciona em duas fases.
A primeira constrói um autômato finito determinístico que reconhece
a linguagem ![]() .
A segunda executa a busca
fornecendo o texto
.
A segunda executa a busca
fornecendo o texto ![]() como entrada para o autômato.
como entrada para o autômato.
Começaremos a construção do autômato com
a construção de uma máquina de estados
que possui um conjunto finito de estados e três funções.
Essa máquina funcionará da seguinte forma: ela recebe uma
palavra ![]() e lê cada símbolo de
e lê cada símbolo de ![]() em seqüência.
Para cada símbolo, ela executa algumas transições de estado e
possivelmente gera uma saída.
De fato, ela é muito semelhante a um autômato finito determinístico,
a diferença é que há duas funções de transição, a usual, que
chamaremos de
em seqüência.
Para cada símbolo, ela executa algumas transições de estado e
possivelmente gera uma saída.
De fato, ela é muito semelhante a um autômato finito determinístico,
a diferença é que há duas funções de transição, a usual, que
chamaremos de ![]() , e a de falha, que chamaremos de
, e a de falha, que chamaremos de ![]() .
A função
.
A função ![]() é usada para ``voltar'' algumas
transições no caso em que a função
é usada para ``voltar'' algumas
transições no caso em que a função ![]() indica
indica ![]() ;
ela tem o mesmo significado da função de falha do
algortimo KMP.
Há também a função
;
ela tem o mesmo significado da função de falha do
algortimo KMP.
Há também a função ![]() , que associa uma saída a cada
estado.
, que associa uma saída a cada
estado.
Para facilitar o nosso estudo, vamos definir a máquina de estados a partir de um autômato finito determinístico.
A máquina de estados é uma tripla
![]() , onde
, onde
Cada ciclo da máquina é definido da forma a seguir.
Seja ![]() o estado atual e
o estado atual e ![]() o símbolo corrente da
entrada
o símbolo corrente da
entrada ![]() .
.
O Algoritmo 12
descreve mais precisamente o
comportamento da máquina.
Para que essa máquina seja capaz de resolver o problema, ela deve satisfazer os requisitos que discutiremos informalmente a seguir.
Além disso, por definição, faremos com que
![]() , para todo
, para todo ![]() tal que
tal que ![]() não foi definido acima.
Para as outras transições
não foi definido acima.
Para as outras transições ![]() não definidas,
onde
não definidas,
onde ![]() e
e
![]() ,
faremos com que
,
faremos com que
![]() .
.
Construiremos primeiro o autômato
![]() , e
nessa construção já é possível definir parte
da função
, e
nessa construção já é possível definir parte
da função
![]() .
Então, a partir de
.
Então, a partir de
![]() , construiremos a função
, construiremos a função ![]() .
A construção definitiva de
.
A construção definitiva de
![]() também será feita
em conjunto com a contrução de
também será feita
em conjunto com a contrução de ![]() .
.
A construção de
![]() será feita a partir da árvore
será feita a partir da árvore ![]() descrita anteriormente.
Inicialmente, a árvore
descrita anteriormente.
Inicialmente, a árvore ![]() só possui o nó raiz, que, lembrando,
representa a palavra vazia.
Para cada palavra
só possui o nó raiz, que, lembrando,
representa a palavra vazia.
Para cada palavra ![]() em
em ![]() , insira
, insira ![]() em
em ![]() da seguinte fo rma.
da seguinte fo rma.
Execute então a finalização a seguir.
O Algoritmo 13
mostra esse procedimento em linguagem mais precisa.
Veja também a Figura 7, que mostra o resultado desse passo da construção da máquina de estados para o dicionário {he, she, hers, his}.
Para a construção de ![]() e o restante de
e o restante de
![]() ,
novamente nos guiaremos pelos requisitos discutidos
anteriormente.
,
novamente nos guiaremos pelos requisitos discutidos
anteriormente.
Usaremos o
Algoritmo 14, que percorre a árvore ![]() como
em uma busca em largura.
Portanto, fica claro que a construção de
como
em uma busca em largura.
Portanto, fica claro que a construção de ![]() é feita
a partir da função
é feita
a partir da função ![]() .
Vamos introduzir então a noção de profundidade.
A profundidade
de um estado
.
Vamos introduzir então a noção de profundidade.
A profundidade
de um estado ![]() em
em ![]() é o tamanho do caminho de
menor comprimento que
começa em
é o tamanho do caminho de
menor comprimento que
começa em ![]() e termina em
e termina em ![]() .
.
O Algoritmo 14
percorre a árvore por nível de profundidade,
começando da profundidade 1.
A função falha de um estado é definida a partir dos estados
das profundidades menores do que a dele.
Podemos já definir inicialmente ![]() para todo
para todo
![]() que tenha profundidade 1.
Suponha agora que
que tenha profundidade 1.
Suponha agora que ![]() já tenha sido definida para
todos os estados de nível menor
do que
já tenha sido definida para
todos os estados de nível menor
do que ![]() .
Sejam
.
Sejam ![]() um estado de nível
um estado de nível ![]() e
e ![]() um estado tal que
um estado tal que
![]() para
algum
para
algum
![]() (
(![]() é de nível
é de nível ![]() ),
queremos definir
),
queremos definir ![]() .
Seja
.
Seja ![]() a palavra representada por
a palavra representada por ![]() em
em ![]() , e
, e ![]() a palavra representada por
a palavra representada por ![]() .
Temos que
.
Temos que
![]() representa o prefixo de maior comprimento
representa o prefixo de maior comprimento
![]() de alguma palavra-chave
que é também um sufixo de
de alguma palavra-chave
que é também um sufixo de ![]() .
O algoritmo então procura pelo estado
.
O algoritmo então procura pelo estado
![]() que representa o prefixo
que representa o prefixo ![]() , tal que
, tal que
![]() , para algum
, para algum
![]() .
Se
.
Se
![]() , então podemos definir
, então podemos definir ![]() .
Caso contrário, consideramos
.
Caso contrário, consideramos ![]() , que também representa
um sufixo de
, que também representa
um sufixo de ![]() que é prefixo de alguma palavra-chave.
Logo, podemos aplicar a mesma idéia até encontrarmos
que é prefixo de alguma palavra-chave.
Logo, podemos aplicar a mesma idéia até encontrarmos
![]() .
Num caso extremo,
.
Num caso extremo,
![]() , pois
, pois
![]() .
.
Ao definirmos ![]() , temos que a palavra
, temos que a palavra ![]() representada
por
representada
por ![]() é um sufixo da palavra
é um sufixo da palavra ![]() representada por
representada por ![]() .
Logo, podemos dizer que
.
Logo, podemos dizer que
![]() deve estar contido
em
deve estar contido
em
![]() .
.
Veja então o Algoritmo 14.
A Figura 8 mostra a máquina de estados (veja também a Figura 7).
Podemos ver que cada passo do laço mais externo do
Algoritmo 12
processa um símbolo de ![]() .
Logo, o número de iterações é
.
Logo, o número de iterações é ![]() .
É visível também que a cada iteração, o algoritmo executa
uma transição
.
É visível também que a cada iteração, o algoritmo executa
uma transição ![]() , então o número de transições usuais
também é
, então o número de transições usuais
também é ![]() .
Temos ainda que o número total de transições de falha não
pode ultrapassar o número de transições usuais em nenhum
momento da execução do algoritmo.
Logo, o número de transições de falha é, no pior caso,
.
Temos ainda que o número total de transições de falha não
pode ultrapassar o número de transições usuais em nenhum
momento da execução do algoritmo.
Logo, o número de transições de falha é, no pior caso, ![]() .
Disso segue que o tempo gasto pelo
Algoritmo 12 é
.
Disso segue que o tempo gasto pelo
Algoritmo 12 é ![]() .
.
Não há muitas dificuldades para observarmos que o
Algoritmo 13 tem complexidade de tempo
![]() .
.
O Algoritmo 14 também possui
complexidade de tempo ![]() , mas
é preciso usar um argumento semelhante ao da
justificativa da busca.
, mas
é preciso usar um argumento semelhante ao da
justificativa da busca.
Portanto, o algoritmo todo,
que compreende a construção e a busca,
tem complexidade de tempo ![]() .
.
Podemos obter um autômato finito determinístico a partir da máquina de estados descrita até agora.
Para isso definiremos a função de transição ![]() de forma
que ela faça o papel das funções
de forma
que ela faça o papel das funções ![]() e
e ![]() .
Note que desse modo a busca fica mais simples, assim como
o cálculo da complexidade de tempo, pois é feita exatamente
uma transição por símbolo da entrada
.
Note que desse modo a busca fica mais simples, assim como
o cálculo da complexidade de tempo, pois é feita exatamente
uma transição por símbolo da entrada ![]() .
.
A idéia é esboçada a seguir.
Sejam ![]() e
e
![]() .
Se
.
Se
![]() , então
podemos dizer que
, então
podemos dizer que
![]() .
Caso contrário, temos simplesmente que
.
Caso contrário, temos simplesmente que
![]() .
.
A descrição completa pode ser vista no Algoritmo 15.
A Figura 9 mostra o autômato final, obtido da máquina de estados da Figura 8.
A complexidade de tempo dessa construção é ![]() .
O número de operações da busca usando a máquina de estados
pode ser reduzido em até metade se usarmos o autômato,
já que o autômato não faz transições de falha.
Porém, não há uma forma confiável de estimar essa redução.
Ademais, a complexidade de tempo da busca é a mesma.
.
O número de operações da busca usando a máquina de estados
pode ser reduzido em até metade se usarmos o autômato,
já que o autômato não faz transições de falha.
Porém, não há uma forma confiável de estimar essa redução.
Ademais, a complexidade de tempo da busca é a mesma.
This document was generated using the LaTeX2HTML translator Version 99.2beta8 (1.42)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -image_type gif -antialias -antialias_text det
The translation was initiated by Leo on 2001-12-10