| Proposta | Pôster | Apresentação | monografia em postscript |
Monografia
Aluno: Leo Kazuhiro Ueda
Supervisora: Nami Kobayashi
Projeto de Iniciação Científica
Autômatos Finitos: Algoritmos e Estruturas de Dados
| Introdução |
Este documento relata a experiência que obtive durante o projeto de iniciação científica realizado ao longo do ano de 2001.
| Autômatos Finitos: Algoritmos e Estruturas de Dados | |
| profa. Nami Kobayashi | |
| março/2001 a dezembro/2001 | |
| PIBIC/CNPq - março/2001 a julho/2001, agosto/2001 a fevereiro/2002 |
| Como começou o projeto |
No final do ano de 2000, eu procurava por um projeto de iniciação científica. Eu visitei páginas de projetos na Rede do IME, e cheguei até a falar com alguns professores. Porém, embora tenha encontrado muitas possibilidades interressantes, eu não conseguia me decidir. O problema era que eu tinha percebido que precisaria de conhecimentos mais específicos para participar desses projetos, ou ao menos para avaliar se eu realmente gostaria de participar deles. A verdade era que eu queria estudar qualquer um dos assuntos, mas não tinha parâmetros para escolher entre tantas opções interessantes.
Naquele semestre, eu estava cursando a disciplina MAC 414 - Autômatos e Linguagens Formais com a profa. Nami. A professora, que já me conhecia, soube que eu estava procurando por uma iniciação científica e me ofereceu ajuda.
A partir daí, eu comecei a olhar projetos que me interessavam e que poderiam se relacionar com Autômatos, que é a área da professora. Eu estudei alguns artigos, mas eu encontrei o mesmo problema de indecisão.
Como eu estava indeciso e parecendo gostar de qualquer assunto, nós formulamos um projeto que me daria um conhecimento básico para eu poder talvez, no futuro, estudar algumas das aplicações mais complicadas que eu havia pesquisado no começo.
E por isso, o objetivo foi simplesmente esse. Nós selecionamos alguns tópicos clássicos em Autômatos Finitos e preparamos o projeto.
| O Projeto |
A Teoria de Autômatos Finitos tem sido aplicada a áreas diversas, como, por exemplo, no desenvolvimento de analisadores léxicos e editores de texto, em Processamento de Imagens, Biologia Molecular Computacional e Lingüística Computacional.
A quantidade e a diversidade dessas aplicações vêm crescendo significativamente, em grande parte devido ao aumento da demanda por sistemas de processamento de quantidades imensas de dados. Como estrutura de dados, um autômato pode armazenar informações de forma a economizar espaço em memória, enquanto isso, os algoritmos já conhecidos para autômatos podem oferecer um processamento eficiente.
Para compreender e estudar essas aplicações, é importante conhecer os algoritmos e estruturas de dados fundamentais que utilizam autômatos finitos. O objetivo deste projeto foi iniciar um estudo de tais aspectos básicos da Teoria de Autômatos Finitos.
Os tópicos estudados até o momento foram:
Além disso, planejamos estudar o Autômato dos Sufixos, mas o estudo está ainda em fase inicial.
| Metodologia |
As atividades foram voltadas basicamente para a compreensão e implementação de cada algoritmo, principalmente através da leitura de artigos e da realização de reuniões semanais. As reuniões envolveram discussões sobre o andamento do projeto, destacando:
| Tópicos Estudados |
Eu havia preparado um texto adaptado do meu relatório parcial para o CNPq [13], especialmente para esta monografia. Infelizmente, não consegui fazer com que esse texto ficasse com um tamanho aceitável. Ele esta disponível aqui [14] como uma referência mais detalhada, mas oficialmente não faz parte da monografia.
Assim, em vez de uma descrição um pouco mais formal, descreverei apenas a idéia dos algoritmos, numa visão bem simplificada. De uma certa maneira, isso deixa de explicitar as maiores dificuldades dos algoritmos, mas espero que seja possível ao menos ter uma noção dessa dificuldade.
| Notação e Definições Básicas |
Antes, precisamos definir uma convenção.
Um autômato finito determinístico![]() é uma quíntupla
é uma quíntupla![]() ,
onde:
,
onde:
Uma palavra é uma seqüência finita de símbolos;
a palavra vazia é denotada por ![]() .
O conjunto de todas as palavras, incluindo
.
O conjunto de todas as palavras, incluindo ![]() ,
é
,
é ![]() .
.
A função ![]() será estendida para
será estendida para![]() da maneira usual:
da maneira usual:
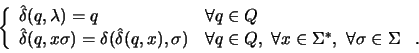
A partir de agora usaremos ![]() para denotar
para denotar ![]() .
.
Diremos também que ![]() é a cardinalidade de
é a cardinalidade de ![]() ,
ou seja, o número de estados de
,
ou seja, o número de estados de ![]() .
.
A linguagem reconhecida por ![]() ,
denotada por
,
denotada por ![]() ,
é o conjunto das palavras
,
é o conjunto das palavras![]() tais que
tais que ![]() .
.
Seja ![]() uma palavras em
uma palavras em ![]() ,
então
,
então ![]() é um prefixo,
é um prefixo, ![]() é um fator e
é um fator e ![]() é um sufixo de
é um sufixo de ![]() ,
para
,
para ![]() ,
, ![]() e
e ![]() em
em ![]() .
.
O grafo associado a ![]() ,
denotado por
,
denotado por ![]() ,
é o grafo orientado
,
é o grafo orientado ![]() ,
onde:
,
onde:
| Minimização de Autômatos Finitos |
Estudamos dois algoritmos para minimização de autômatos
finitos determinísticos, a versão de David Gries para o algoritmo
de John Hopcroft, com complexidade de tempo ![]() ,
e o algoritmo de Dominique Revuz para autômatos acíclicos,
com complexidade
,
e o algoritmo de Dominique Revuz para autômatos acíclicos,
com complexidade ![]() .
.
O problema que queremos resolver é minimizar o número
de estados de um autômato finito determinístico. Isto é,
dado um autômato ![]() ,
queremos determinar um autômato
,
queremos determinar um autômato ![]() com o menor número de
estados e tal que
com o menor número de
estados e tal que ![]() .
Tal autômato
.
Tal autômato ![]() é chamado de minimal.
é chamado de minimal.
Os métodos utilizados pelos dois algoritmos que estudamos se
baseiam na seguinte relação de equivalência sobre ![]() :
:
Definição 1 Dois estadosDe modo muito simplificado, os algoritmos procuram pelas classes de equivalência eme
são equivalentes se, e somente se, para todo
, vale que
.
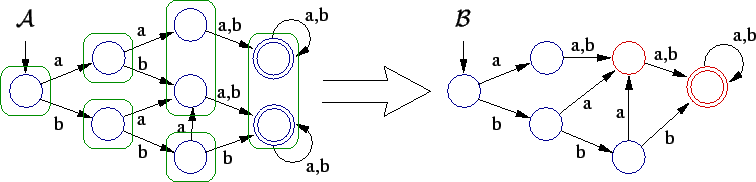
As classes de equivalência em ![]() estão marcadas com a cor verde, repare que cada classe é
um estado em
estão marcadas com a cor verde, repare que cada classe é
um estado em ![]() .
Portanto, se encontrarmos as classes de equivalência, teremos minimizado
o autômato.
.
Portanto, se encontrarmos as classes de equivalência, teremos minimizado
o autômato.
Em [8], Hopcroft apresenta um algoritmo para
minimizar o número de estados de um autômato finito determinístico,
e afirma que ele tem complexidade de tempo ![]() .
.
Até aquele momento, os algoritmos conhecidos levavam tempo ![]() ,
ou mais, no pior caso. Porém, a descrição do novo
algoritmo e as suas provas de corretude e complexidade de tempo foram consideradas
complicadas demais.
,
ou mais, no pior caso. Porém, a descrição do novo
algoritmo e as suas provas de corretude e complexidade de tempo foram consideradas
complicadas demais.
Por muitos anos, a despeito da importante melhora em relação
aos algoritmos clássicos, o algoritmo de Hopcroft foi praticamente
omitido de textos básicos sobre autômatos finitos. Alguns
apenas descreviam o algoritmo, mas sem mostrar as provas de complexidade
e corretude. Muitos dos textos básicos [9,11]
continuaram a apresentar somente os algoritmos ![]() .
.
Com o objetivo de fornecer uma descrição mais clara, David Gries [7] redescreve o algoritmo de Hopcroft, mas com uma pequena modificação. Apesar de ter cumprido seu objetivo, a descrição de Gries não se tornou muito popular.
Nosso estudo foi centrado no artigo de Gries.
Para encontrar as classes de equivalência, o algoritmo de Hopcroft
começa com uma partição dos estados do autõmato ![]() .
Essa partição é formada por dois blocos: um contendo
os estados finais e outro contendo os não-finais.
.
Essa partição é formada por dois blocos: um contendo
os estados finais e outro contendo os não-finais.
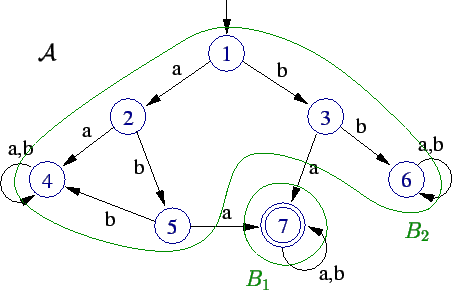
Cada passo do algoritmo é um refinamento dos blocos da partição. Os blocos são divididos de forma que os estados equivalentes permanecem em blocos iguais. Podemos ver que na situação inicial isso é verdade, pois um estado final não pode ser equivalente a um estado não-final.
A Figura 3 mostra a divisão
do bloco ![]() em relação ao bloco
em relação ao bloco ![]() e ao símbolo
e ao símbolo ![]() .
.
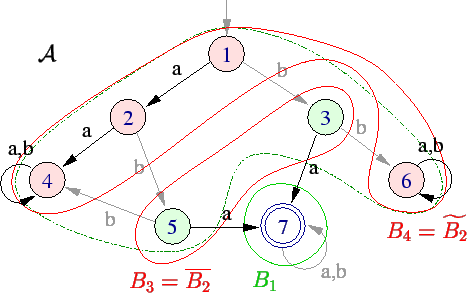
No bloco ![]() ficaram os estados que possuem uma transição com rótulo
ficaram os estados que possuem uma transição com rótulo ![]() que vai para algum estado do bloco
que vai para algum estado do bloco ![]() .
No bloco
.
No bloco ![]() ficaram os estados que não possuem tal transição.
Dessa forma, os estados equivalentes de fato permanecem no mesmo bloco.
No final, teremos que cada bloco da partição representa uma
classe de equivalência, ou seja, em cada bloco, todos os estados
são equivalentes entre si. Veja o resto das divisões relevantes.
ficaram os estados que não possuem tal transição.
Dessa forma, os estados equivalentes de fato permanecem no mesmo bloco.
No final, teremos que cada bloco da partição representa uma
classe de equivalência, ou seja, em cada bloco, todos os estados
são equivalentes entre si. Veja o resto das divisões relevantes.
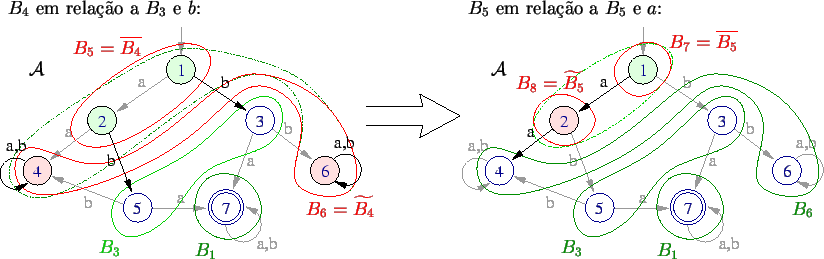
Temos então as classes de equivalência, e portanto o autômato minimal.
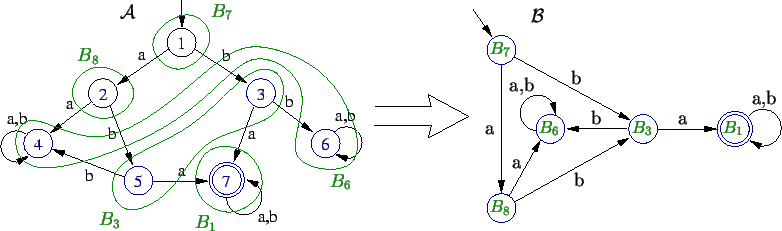
A característica mais importante do algoritmo é a ordem em que são feitas essas divisões, mais precisamente, como ela é definida. Uma discussão sobre isso pode ser vista aqui [14].
Em seu artigo, Gries propõe uma possível implementação
das estruturas de dados. As estruturas dessa proposta são bem simples,
são baseadas em vetores pré-alocados, por isso nós
seguimos essa proposta em nossa implementação. O espaço
em memória utilizado por elas é ![]() .
.
Um autômato determinístico ![]() é acíclico se o grafo
é acíclico se o grafo ![]() é acíclico. Autômatos determinísticos acíclicos
são bastante usados para representar dicionários [2]
e manipular funções booleanas [3].
é acíclico. Autômatos determinísticos acíclicos
são bastante usados para representar dicionários [2]
e manipular funções booleanas [3].
O algoritmo de Revuz tem grande importância para essas aplicações,
pois além de diminuir o espaço em memória utilizado
e agilizar as buscas com autômatos, ele tem complexidade de tempo ![]() .
.
O algoritmo começa calculando uma partição![]() dos estados de
dos estados de ![]() .
Os estados de um bloco
.
Os estados de um bloco ![]() possuem altura
possuem altura![]() .
A altura de um estado é o tamanho do caminho de maior comprimento
que começa no estado e chega a um estado final. Note, portanto,
que é possível calcular
.
A altura de um estado é o tamanho do caminho de maior comprimento
que começa no estado e chega a um estado final. Note, portanto,
que é possível calcular ![]() fazendo uma busca em largura no grafo
fazendo uma busca em largura no grafo ![]() .
.
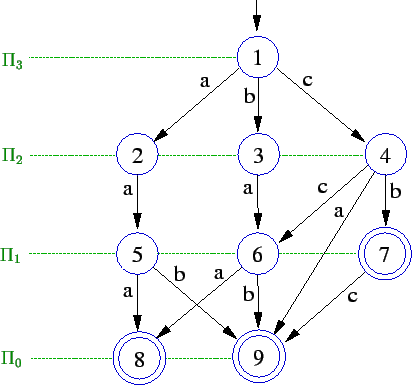
Repare que estados de alturas diferentes não podem ser equivalentes.
A idéia do algoritmo é nomear cada estado com uma palavra
que descreve as suas transições, de forma que dois estados
possuem nomes iguais se e somente se eles são equivalentes. Tendo
isso, o algoritmo percorre os blocos![]() nessa ordem, aplicando uma ordenação lexicográfica
nos nomes dos estados de cada bloco
nessa ordem, aplicando uma ordenação lexicográfica
nos nomes dos estados de cada bloco ![]() ,
e dessa forma encontrando os estados com nomes iguais. Os estados equivalentes
são então unidos, formando um único estado.
,
e dessa forma encontrando os estados com nomes iguais. Os estados equivalentes
são então unidos, formando um único estado.
Veja o exemplo de execução.
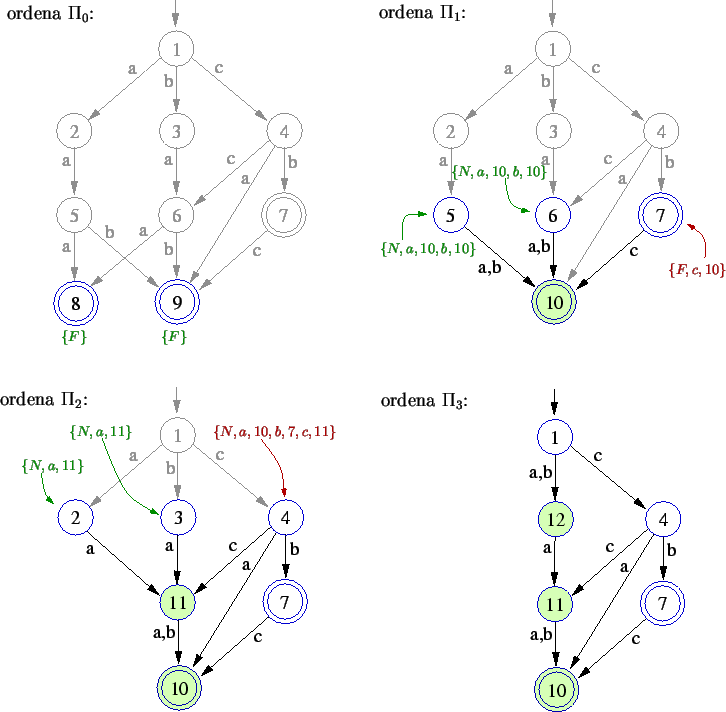
Para termos complexidade de tempo linear, precisamos de um algoritmo também de tempo linear. Não apenas isso, os nomes dados aos estados também devem possuir tamanho linear, de uma certa forma. Detalhes disso podem ser vistos aqui [14].
O algoritmo precisa de espaço em memória para armazenar
o autômato e para realizar a ordenação linear. A soma
de ambos é ![]() .
.
| Um problema de busca de padrões |
Neste projeto estudamos também um problema particular de busca de
padrões em textos. Trata-se do caso em que o padrão é
um conjunto finito ![]() de palavras.
de palavras.
O nosso estudo foi centrado no algoritmo clássico de Alfred Aho e Margaret Corasick. Em [1] eles apresentam o algoritmo, tendo como motivação a otimização de um sistema de consulta a um banco de dados de referências bibliográficas. Os resultados em relação aos algoritmos convencionais da época foram excelentes. Outras descrições do algoritmo podem ser encontradas em [4,5].
Vamos então descrever o problema e o modelo de solução,
que envolve a construção de um autômato finito determinístico
que representa as palavras em ![]() .
Para essa construção foram aplicadas algumas idéias
do algoritmo KMP, de Knuth, Morris e Pratt [10].
Esse algoritmo resolve o problema da busca de padrões para o caso
em que o padrão é uma palavra.
.
Para essa construção foram aplicadas algumas idéias
do algoritmo KMP, de Knuth, Morris e Pratt [10].
Esse algoritmo resolve o problema da busca de padrões para o caso
em que o padrão é uma palavra.
Seja ![]() um conjunto finito de palavras em
um conjunto finito de palavras em ![]() ,
as quais chamaremos de palavras-chave, e
,
as quais chamaremos de palavras-chave, e ![]() ,
também em
,
também em ![]() ,
uma palavra qualquer que chamaremos de texto. O problema que queremos
resolver é localizar e identificar todos os fatores de
,
uma palavra qualquer que chamaremos de texto. O problema que queremos
resolver é localizar e identificar todos os fatores de ![]() que são também palavras-chave. Em outras palavras,
queremos saber quais palavras do dicionário
que são também palavras-chave. Em outras palavras,
queremos saber quais palavras do dicionário ![]() ocorrem no texto
ocorrem no texto![]() .
.
Para isso, utilizaremos um autômato que reconhece a linguagem ![]() .
O autômato recebe como entrada o texto
.
O autômato recebe como entrada o texto![]() e gera uma saída contendo as posições em
e gera uma saída contendo as posições em ![]() onde alguma palavra-chave aparece como fator. Essa fase é
a busca propriamente dita, e sua complexidade de tempo é
onde alguma palavra-chave aparece como fator. Essa fase é
a busca propriamente dita, e sua complexidade de tempo é ![]() ,
mas pode depender de
,
mas pode depender de ![]() ,
conforme a implementação da função de transição.
Note que esse tempo não depende do número de
palavras-chave.
,
conforme a implementação da função de transição.
Note que esse tempo não depende do número de
palavras-chave.
Há também a fase de construção do autômato.
Ela é feita em duas etapas, em tempo ![]() no total, onde
no total, onde ![]() é a soma dos comprimentos das palavras em
é a soma dos comprimentos das palavras em ![]() .
A primeira etapa consiste em construir, a partir do conjunto
.
A primeira etapa consiste em construir, a partir do conjunto ![]() ,
uma máquina de estados muito semelhante a um autômato finito
determinístico. Essa construção utiliza as idéias
do algoritmo KMP, e pode ser feita em tempo
,
uma máquina de estados muito semelhante a um autômato finito
determinístico. Essa construção utiliza as idéias
do algoritmo KMP, e pode ser feita em tempo![]() ,
dependendo da implementação. Em seguida, a partir da máquina
de estados, pode-se obter em tempo
,
dependendo da implementação. Em seguida, a partir da máquina
de estados, pode-se obter em tempo ![]() o autômato finito determinístico, que reconhece a linguagem
o autômato finito determinístico, que reconhece a linguagem ![]() .
.
Podemos ver que o tempo de construir e aplicar a máquina de estados
é ![]() .
Note que aplicando o algoritmo KMP
.
Note que aplicando o algoritmo KMP ![]() vezes com entrada
vezes com entrada ![]() ,
uma vez para cada palavra em
,
uma vez para cada palavra em ![]() ,
a complexidade total de pior caso seria
,
a complexidade total de pior caso seria ![]() .
.
Como já mencionamos, o algoritmo Aho-Corasick inicialmente constrói
um autômato que reconhece a linguagem ![]() .
Essa construção é feita em etapas, a primeira constrói
um autômato que reconhece as palavras-chave. Vejamos um exemplo
para
.
Essa construção é feita em etapas, a primeira constrói
um autômato que reconhece as palavras-chave. Vejamos um exemplo
para ![]() .
.
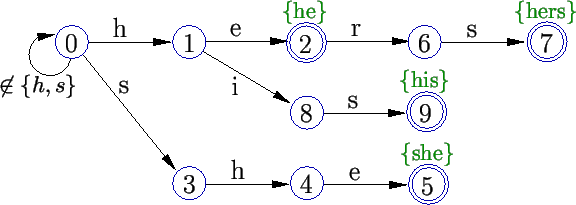
A partir dessa estrutura, o algoritmo constrói uma máquina de estados semelhante a um autômato. A diferença dessa máquina é que ela possui uma segunda função de transição, chamada falha. Essa função utiliza as mesmas idéias do algoritmo KMP.
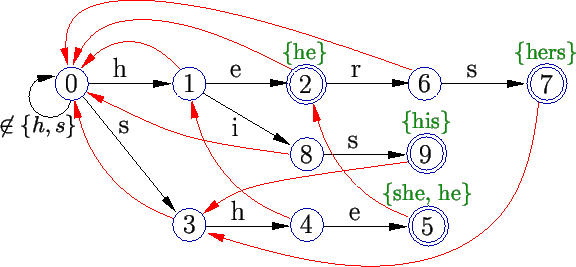
Numa busca do texto na máquina de estados, a transição
de falha de um estado é usada quando a transição ![]() não está definida para esse estado. Ela indica o estado para
o qual devemos voltar e repetir a busca. Por exemplo, numa busca no texto
``shine'', passaríamos pelos estados nesta ordem:
não está definida para esse estado. Ela indica o estado para
o qual devemos voltar e repetir a busca. Por exemplo, numa busca no texto
``shine'', passaríamos pelos estados nesta ordem: ![]() (confira na Figura 9). Note que
a máquina já é capaz de reconhecer
(confira na Figura 9). Note que
a máquina já é capaz de reconhecer ![]() ,
ou seja, pode resolver o problema.
,
ou seja, pode resolver o problema.
A última fase é a construção de um autômato finito determinístico a partir da máquina de estados.
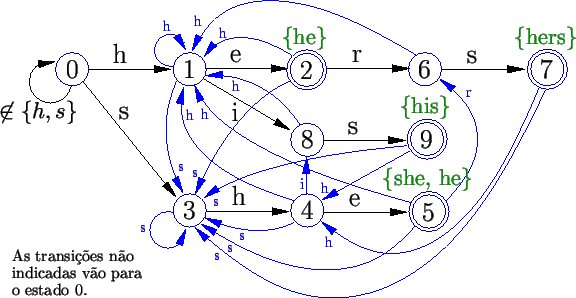
Vejamos novamente a busca das palavras do dicionário no texto
``shine'', mas desta vez no autômato da Figura 10: ![]() .
Não há ocorrência de nenhuma palavra-chave no
texto ``shine''. Podemos notar também que o autômato
utiliza um pouco menos transições em comparação
com a máquina de estados. Porém, tanto o autômato quanto
a máquina utilizam
.
Não há ocorrência de nenhuma palavra-chave no
texto ``shine''. Podemos notar também que o autômato
utiliza um pouco menos transições em comparação
com a máquina de estados. Porém, tanto o autômato quanto
a máquina utilizam ![]() transições numa busca em
transições numa busca em ![]() (ou seja, a complexidade não muda). Ademais, a quantidade de transições
do autômato é bem maior (
(ou seja, a complexidade não muda). Ademais, a quantidade de transições
do autômato é bem maior (![]() contra
contra ![]() ).
).
| O Autômato dos Sufixos |
O estudo do Autômato dos Sufixos ainda está em fase inicial. Até agora estudamos apenas tópicos relacionados:
| Implementações |
Nós implementamos os três algoritmos estudados na linguagem C, padrão ANSI. Embora essas implementações tivessem como objetivo auxiliar o entendimento das questões de complexidade de tempo e de espaço, elas geraram discussões interessantes sobre outras questões. Algumas delas foram:
Com uma pequena adaptação, a estrutura da Figura 8, gerada pelo algoritmo Aho-Corasick, pode se transformar numa árvore que armazena um dicionário. Essa árvore consegue responder rapidamente se uma palavra pertence ao dicionário.
Uma possibilidade mais interessante é utilizar um dos algoritmos de minimização para que essa representação utilize menos memória. Como essa árvore é um autômato acíclico, foi possível utilizar o algoritmo de Revuz.
| Gerado pelo Aho-Corasick | Minimizado pelo Revuz | |||||||
| Palavras | Estados | Transições | Tempo | Estados | Transições | Tempo | ||
| 40000 | 77581 | 77580 | 4,660s | 3965 | (5,11%) | 8955 | (11,54%) | 4,880s |
| 80000 | 154452 | 154451 | 9,570s | 6940 | (4,49%) | 16668 | (10,79%) | 9,840s |
| 160000 | 308323 | 308322 | 19,260s | 12415 | (4,03%) | 31812 | (10,32%) | 19,710s |
| 198769 | 382803 | 382802 | 23,800s | 14559 | (3,80%) | 37619 | (9,88%) | 24,260s |
As porcentagens mostram a diminuição significativa do número de estados e de transições, e os tempos de execução fornecem indícios de que os algoritmos são de fato lineares.
O autômato gerado pelo algoritmo Aho-Corasick ocupa um espaço considerável de memória, então discutimos se não valeria a pena minimizar o autômato produzido pelo algoritmo Aho-Corasick. Notamos que dessa forma perderíamos a informação de qual palavra ocorre em certo ponto do texto, o que resultaria num aumento da complexidade de tempo da busca. Não sabemos, porém, se na prática essa troca de espaço por tempo compensa.
| Desafios, Frustrações e Considerações Pessoais |
As dificuldades apareceram nas principais atividades deste projeto, que foram a leitura de artigos e a produção do relatório. Eu esperava por isso, já que, antes de começar o projeto, tinha tido muito pouca ou nenhuma experiência parecida no curso.
Mas, com o passar do tempo e com a orientação da profa. Nami, eu pude perceber que, apesar disso, o curso havia sim me preparado para aqueles tipos de atividades. Em outras palavras, as atividades do curso foram diferentes das atividades da iniciação, entretanto, a experiência obtida no curso permitiu que eu realizasse as atividades da iniciação.
Com isso, o desafio passou a ser a própria dificuldade de entender os artigos, e a base teórica obtida no curso foi fundamental para superá-lo. Ela também me ajudou a lidar com outros problemas, como deficiências e até erros nos artigos.
Porém, o trabalho neste projeto foi praticamente individual, e essa foi uma grande frustração. Eu cheguei a receber conselhos importantes do aluno de mestrado da profa. Nami, Rodrigo de Souza, mas não chegamos a trabalhar juntos.
O único trabalho em grupo eram as reuniões semanais, onde eu discutia com a profa. Nami o trabalho que tinha sido feito. Essa interação foi um dos aspectos mais valiosos do projeto. Nessas reuniões, por exemplo, discutíamos detalhes dos artigos lidos, e nessa interação eu não era simplesmente ensinado pela professora, mas também aprendia fatos novos junto com ela. Essa foi de fato uma experiência totalmente nova em relação às que eu conheci no BCC.
Ademais, o apoio da profa. Nami foi de grande importância para mim. Não foi só um apoio como orientadora da iniciação científica, ela também me aconselhou em questões sobre o curso.
Outra grande frustração foi que os resultados foram apenas para o meu benefício, o objetivo do projeto não incluía a produção de algo que pudesse ser útil para as outras pessoas. Há um ano eu estava desnorteado pela minha indecisão, não percebi que esse era um aspecto importante, e que eu sentiria falta disso. No entanto, o meu objetivo a longo prazo era justamente poder trabalhar num projeto com tais resultados, e por isso acredito que essa frustração não invalida este projeto.
| Disciplinas Relevantes |
Ao cursar uma disciplina, tento não ver o conhecimento que ela pode me fornecer como um fator principal. O que mais valorizo numa disciplina são as novas idéias e conceitos que eu posso adquirir, a absorção do conhecimento específico seria apenas uma conseqüência desejável. Nesse sentido, considero que quase todas as disciplinas foram relevantes para este projeto.
Mas é claro que posso listar as disciplinas que tiveram alguma aplicação direta no meu trabalho.
MAC 414 - Autômatos e Linguagens Formais e MAC 328 - Algoritmos em Grafos
Foram as mais importantes, os tópicos estudados no projeto pressupunham conhecimentos obtidos nessas disciplinas.
MAC 338 - Análise de Algoritmos e MAC 331 - Geometria Computacional
Foram importantes para as análises dos algoritmos. A disciplina Geometria Computacional foi útil porque no semestre em que cursei (com o prof. Coelho) foi dada uma ênfase para análise de algoritmos.
Uma disciplina que não teve aplicação direta, mas que teve uma importância destacável, foi MAC 315 - Programação Linear, com o prof. Leônidas. Pelo modo como ela foi dada, eu tive a chance de amadurecer a minha capacidade compreender e construir demonstrações matemáticas. E isso sim foi aplicado diretamente no projeto. É verdade que eu tive a mesma chance em muitas outras disciplinas, mas essa disciplina em especial foi marcante nesse aspecto.
| Conclusão |
O Trabalho de Formatura foi uma ótima oportunidade para que eu realizasse um projeto grande e tivesse, talvez, uma noção da qualidade da formação oferecida pelo BCC. Foi também, sem dúvida, a ocasião em eu mais apliquei e obtive conhecimentos.
O projeto de iniciação científica ainda não está concluído, ainda prevê atividades até fevereiro de 2002. Depois disso pretendo continuar meus estudos, mas provavelmente não nessa área. Ainda não decidi a minha área de preferência, apenas sei que vou continuar estudando simplesmente porque gosto de aprender.
| Referências |
| About this document ... |
This document was generated using the
LaTeX2HTML
translator Version 99.2beta8 (1.42)
(Não completamente, tive que arrumar muitas coisas!)
Copyright © 1993, 1994, 1995, 1996,
Nikos
Drakos, Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross
Moore, Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -image_type gif -antialias -antialias_text
mono
The translation was initiated by Leo on 2001-12-10
A tradução não ficou muito boa, há uma versão ps disponível...